Pierwiastkowanie liczb zespolonych
Wyciąganie pierwiastka stopnia $n$ z liczby zespolonej określamy jako działania odwrotne do potęgowania, wykonuje się według wzoru de Moivre'a dla ułamkowego wykładnika potęgi, tzn jeżeli $z=|z|(cos\varphi+i\sin\varphi)$ oraz $n$ jest liczbą naturalną, to:
$$\sqrt[n]{z}=\sqrt[n]{|z|}\left(\cos\frac{\varphi+2k\pi}{n}+i\sin\frac{\varphi+2k\pi}{n}\right)$$
Dodawanie, odejmowanie, mnożenie, dzielenie liczb zespolonych oraz podnoszenie liczb zespolonych do potęgi o wykładniku całkowitym są działaniami jednoznacznymi, natomiast wyciąganie pierwiastka stopnia $n$, gdzie $n$ jest liczbą naturalną, daje zawsze $n$ różnych wartości. Jeżeli bowiem do powyższego wzoru podstawiać będziemy $k=0, 1, 2, ..., n-1$, to argument $\sqrt[n]{z}$ przybierać będzie wartości:
$$\frac{\varphi}{n}\text{,}\quad \frac{\varphi+2\pi}{n}\text{,}\quad \frac{\varphi+4\pi}{n}\text{,}\quad ...\text{,}\quad \frac{\varphi +2(n-1)\pi}{n}$$
różniące się o $\frac{2\pi}{n}$, przy dalszych wartościach $k$ wartość argumentu $\sqrt[n]{z}$ będą się okresowo powtarzały.
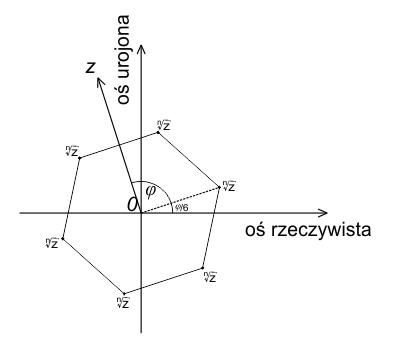
W interpretacji geometrycznej punkty przedstawiające $\sqrt[n]{z}$ są wierzchołkami $n$-kąta foremnego mającego środek w biegunie.
Na poniższym rysunku przedstawiono sześć wartości $\sqrt[6]{z}$.