Czworokąt
Czworokąt to figura geometryczna na płaszczyźnie, która posiada cztery boki i cztery kąty. Czworokąty są jednymi z najczęściej spotykanych figur w geometrii, a ich właściwości zależą od wzajemnych relacji pomiędzy bokami i kątami. Przykładem dowolnego czworokąta jest figura przedstawiona poniżej:
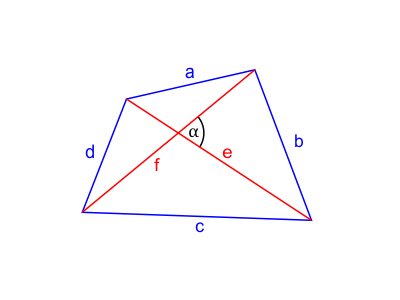
Na rysunku oznaczono:
- $a$, $b$, $c$, $d$ – długości boków czworokąta,
- $e$, $f$ – długości przekątnych czworokąta,
- $\alpha$ – miara kąta zawartego pomiędzy przekątnymi $e$ i $f$.
Obwód czworokąta
Obwód czworokąta to suma długości wszystkich jego boków. Niezależnie od kształtu czworokąta, obwód można obliczyć za pomocą wzoru:
$$Obw = a + b + c + d$$
gdzie $a$, $b$, $c$, $d$ to długości poszczególnych boków czworokąta.
Pole czworokąta
Pole dowolnego czworokąta można obliczyć, znając długości jego przekątnych oraz kąt między nimi. Wzór na pole czworokąta to:
$$P = \frac{e \cdot f}{2} \sin \alpha$$
gdzie:
- $e$ i $f$ to długości przekątnych czworokąta,
- $\alpha$ to kąt zawarty pomiędzy przekątnymi.
Ten wzór jest szczególnie użyteczny, gdy nie znamy długości boków czworokąta, ale mamy informacje o jego przekątnych i kącie między nimi.
Podsumowanie
Czworokąty to wszechstronne figury geometryczne, które mogą przybierać różnorodne kształty, od prostych prostokątów po bardziej skomplikowane formy. Zrozumienie, jak obliczać obwód i pole czworokąta, jest kluczowe w geometrii oraz w praktycznych zastosowaniach, takich jak projektowanie i analiza kształtów.