Postać trygonometryczna liczby zespolonej

Postać trygonometryczna liczby zespolonej to sposób zapisu liczby zespolonej za pomocą jej modułu i argumentu. W tej postaci liczba zespolona $z$ jest wyrażona wzorem:

$$ z = |z|(\cos \varphi + i \sin \varphi) $$

gdzie:

• $|z|$ – jest modułem (wartością bezwzględną) liczby zespolonej, czyli długością promienia wodzącego od początku układu współrzędnych do punktu reprezentującego tę liczbę na płaszczyźnie zespolonej.
• $\varphi$ – jest argumentem liczby zespolonej, czyli kątem między osią rzeczywistą (biegunową) a promieniem wodzącym, wyrażonym w mierze łukowej. Argument liczby zespolonej przyjmuje wartości w przedziale $\varphi \in (-\pi, \pi\rangle$.

Interpretacja geometryczna postaci trygonometrycznej

Postać trygonometryczna liczby zespolonej wynika z reprezentacji liczby zespolonej na płaszczyźnie zespolonej w układzie współrzędnych biegunowych. W układzie tym punkt $z = a + bi$ jest opisany przez współrzędne biegunowe $(|z|, \varphi)$, gdzie $|z|$ to odległość punktu od początku układu współrzędnych (moduł liczby zespolonej), a $\varphi$ to kąt między osią rzeczywistą a wektorem wodzącym (argument liczby zespolonej).

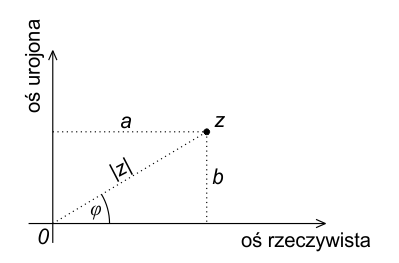
Przechodząc od współrzędnych kartezjańskich $(a, b)$ do współrzędnych biegunowych $(|z|, \varphi)$, korzystamy z następujących wzorów:

• Moduł liczby zespolonej: $$ |z| = \sqrt{a^2 + b^2} $$
• Argument liczby zespolonej: $$ \cos{\varphi} = \frac{a}{|z|}, \quad \sin{\varphi} = \frac{b}{|z|} $$

W szczególności, jeżeli $|z| \neq 0$, współrzędne kartezjańskie $a$ i $b$ mogą być wyrażone jako:

$$ a = |z|\cos{\varphi}, \quad b = |z|\sin{\varphi} $$

Właściwości postaci trygonometrycznej

• Argument liczby zespolonej: Dla liczby zespolonej $z = a + bi$, argument $\varphi$ określa kąt, pod jakim promień wodzący od początku układu współrzędnych do punktu $(a, b)$ przecina oś rzeczywistą. Argument może przyjmować wiele wartości, ponieważ dodanie dowolnej wielokrotności $2\pi$ do argumentu również daje prawidłowy kąt. Wartość główna argumentu liczby zespolonej jest jednak zawarta w przedziale $-\pi < \varphi \leqslant \pi$.
• Równoważność postaci trygonometrycznej i algebraicznej: Postać trygonometryczna jest równoważna postaci algebraicznej liczby zespolonej. Przechodząc między tymi dwiema postaciami, używamy równań łączących współrzędne kartezjańskie $(a, b)$ z współrzędnymi biegunowymi $(|z|, \varphi)$: $$ z = a + bi = |z|(\cos{\varphi} + i\sin{\varphi}) $$
• Operacje na liczbach zespolonych w postaci trygonometrycznej: Postać trygonometryczna jest szczególnie przydatna do wykonywania operacji takich jak mnożenie i dzielenie liczb zespolonych. W tej postaci: $$ z_1 \cdot z_2 = |z_1||z_2| \left( \cos(\varphi_1 + \varphi_2) + i\sin(\varphi_1 + \varphi_2) \right) $$ $$ \frac{z_1}{z_2} = \frac{|z_1|}{|z_2|} \left( \cos(\varphi_1 - \varphi_2) + i\sin(\varphi_1 - \varphi_2) \right) $$

Przykłady zastosowania postaci trygonometrycznej

Postać trygonometryczna liczb zespolonych jest szeroko stosowana w matematyce i naukach inżynieryjnych, na przykład:

• Analiza sygnałów: W teorii sygnałów liczby zespolone w postaci trygonometrycznej są używane do reprezentacji sygnałów sinusoidalnych o różnych amplitudach i fazach.
• Elektrotechnika: W analizie obwodów prądu zmiennego, liczby zespolone reprezentują napięcia i prądy o różnych amplitudach i fazach, a postać trygonometryczna ułatwia obliczenia.
• Fizyka kwantowa: W mechanice kwantowej, liczby zespolone w postaci trygonometrycznej są używane do opisu stanów kwantowych i operatorów.

Podsumowanie

Postać trygonometryczna liczby zespolonej jest jednym z podstawowych sposobów reprezentacji liczb zespolonych, szczególnie użytecznym w obliczeniach związanych z wielkościami wektorowymi i kątowymi. Zrozumienie tej postaci pozwala na bardziej intuicyjne operowanie liczbami zespolonymi oraz łatwiejsze wykonywanie operacji matematycznych i fizycznych.