Dodawanie liczb zespolonych

Dodawanie dwóch liczb zespolonych jest podstawową operacją w algebrze liczb zespolonych. Aby dodać dwie liczby zespolone $z_1$ i $z_2$, sumujemy ich części rzeczywiste oraz sumujemy ich części urojone. Formalnie, jeśli mamy dwie liczby zespolone $z_1 = a_1 + b_1i$ oraz $z_2 = a_2 + b_2i$, to ich suma $z = z_1 + z_2$ jest dana wzorem:

$$ z_1 + z_2 = (a_1 + b_1i) + (a_2 + b_2i) = (a_1 + a_2) + (b_1 + b_2)i $$

W tym wzorze:

• $a_1$ i $a_2$ – części rzeczywiste liczb zespolonych $z_1$ i $z_2$
• $b_1$ i $b_2$ – części urojone liczb zespolonych $z_1$ i $z_2$

Aby dodać dwie liczby zespolone, należy zatem dodać do siebie ich części rzeczywiste oraz dodać do siebie ich części urojone:

$$ (a_1 + a_2) \quad \text{i} \quad (b_1 + b_2)i $$

Interpretacja geometryczna dodawania liczb zespolonych

Dodawanie liczb zespolonych ma również intuicyjne wyjaśnienie geometryczne na płaszczyźnie zespolonej. Każda liczba zespolona $z = a + bi$ może być przedstawiona jako punkt lub wektor na płaszczyźnie, gdzie $a$ jest współrzędną rzeczywistą (oś x), a $b$ współrzędną urojoną (oś y).

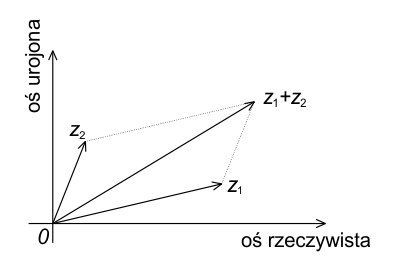
Aby znaleźć sumę dwóch liczb zespolonych $z_1$ i $z_2$ na płaszczyźnie zespolonej, dodajemy ich wektory metodą równoległoboku. Wektor sumy $z = z_1 + z_2$ jest wtedy przekątną równoległoboku, którego boki wyznaczają wektory $z_1$ i $z_2$.

Przykład dodawania liczb zespolonych

Rozważmy dwa przykłady dodawania liczb zespolonych:

• Przykład 1: Dodajmy liczby zespolone $z_1 = 3 + 2i$ oraz $z_2 = 1 + 4i$. Suma tych liczb to: $$ z_1 + z_2 = (3 + 2i) + (1 + 4i) = (3 + 1) + (2 + 4)i = 4 + 6i $$
• Przykład 2: Dodajmy liczby zespolone $z_1 = -2 + 3i$ oraz $z_2 = 5 - 7i$. Suma tych liczb to: $$ z_1 + z_2 = (-2 + 3i) + (5 - 7i) = (-2 + 5) + (3 - 7)i = 3 - 4i $$

Właściwości dodawania liczb zespolonych

Dodawanie liczb zespolonych ma kilka ważnych właściwości, które są analogiczne do właściwości dodawania liczb rzeczywistych:

• Łączność: Dla dowolnych liczb zespolonych $z_1$, $z_2$ i $z_3$: $$ (z_1 + z_2) + z_3 = z_1 + (z_2 + z_3) $$
• Przemienność: Dla dowolnych liczb zespolonych $z_1$ i $z_2$: $$ z_1 + z_2 = z_2 + z_1 $$
• Istnienie elementu neutralnego: Liczba zespolona $0 + 0i$ jest elementem neutralnym dodawania: $$ z + 0 = z $$ dla dowolnej liczby zespolonej $z$.
• Istnienie elementu przeciwnego: Dla każdej liczby zespolonej $z = a + bi$, istnieje liczba zespolona $-z = -a - bi$ taka, że: $$ z + (-z) = 0 $$

Podsumowanie

Dodawanie liczb zespolonych jest podstawową operacją algebraiczną, która polega na dodaniu odpowiednich części rzeczywistych i urojonych. Jest to operacja przemienna i łączna, a jej interpretacja geometryczna jako dodawanie wektorów na płaszczyźnie zespolonej ułatwia wizualizację tej operacji. Znajomość tej operacji jest niezbędna do pracy z liczbami zespolonymi w matematyce, fizyce i inżynierii.