Liczby

Liczba (liczby) to podstawowe pojęcie matematyki, które powstało w świadomości człowieka na wiele tysięcy lat przed naszą erą. Kształtowało się i rozwijało wraz z rozwojem całej cywilizacji i kultury. Kiedy proste rozróżnienie między "jeden" a "wiele", charakterystyczne dla ludów pierwotnych, przestało wystarczać, wprowadzone zostały liczby $1$, $2$, $3$, $4$, ..., czyli liczby naturalne (tzn. liczby całkowite i liczby dodatnie). Zaznaczanie liczb naturalnych odbywało się przez nacinanie kości zwierzęcych, kijów, patyków, a także innych przedmiotów życia codziennego.

Rozwój pojęcia liczby

Wraz z rozwojem piśmiennictwa powstał zapis liczb w odpowiednich systemach liczbowych przy użyciu umownych znaków oraz cyfr. Już w dziełach Euklidesa i Archimedesa zawarte zostało spostrzeżenie, że proces tworzenia coraz większych liczb naturalnych jest nieskończony. Archimedes opracował nawet metodę zapisywania i nazywania liczb większych niż "liczba ziaren piasku na świecie".

Początki arytmetyki

Ustalenie zasad dodawania, odejmowania, mnożenia i dzielenia liczb naturalnych oraz poznanie własności tych działań zapoczątkowało rozwój arytmetyki. Pierwszym rozszerzeniem pojęcia liczb było wprowadzenie ułamków (np. $\frac{1}{2}$, $\frac{1}{3}$, $\frac{3}{4}$, $\frac{7}{13}$), dzięki którym stało się możliwe dzielenie liczb naturalnych.

Liczby ujemne i zero

Na przełomie wieków VI-XI w Indiach wprowadzono liczby ujemne oraz pojęcie zera, co umożliwiło odejmowanie liczb naturalnych bez wcześniejszych ograniczeń. Geometryczną interpretację liczb ujemnych jako wektorów na osi liczbowej, skierowanych przeciwnie do kierunku osi, podał Descartes. Dzięki niemu liczby ujemne rozpowszechniły się w całej Europie.

Liczby całkowite i wymierne

Liczby naturalne oraz odpowiadające im liczby ujemne: $-1$, $-2$, $-3$, $-4$, $-5$, ..., oraz zero ($0$) nazywane są łącznie liczbami całkowitymi. Zbiór liczb całkowitych oraz zbiór ułamków (dodatnich oraz ujemnych) tworzą zbiór liczb wymiernych. Zbiór liczb wymiernych posiada własność gęstości, co oznacza, że dla dwóch różnych liczb wymiernych $a$ i $b$ zawsze istnieje liczba wymierna $c$ taka, że $a < c < b$, czyli pomiędzy dwoma liczbami można zawsze znaleźć trzecią - większą od $a$ i mniejszą od $b$.

Liczby niewymierne i rzeczywiste

Zbiór liczb wymiernych nie wystarczał jednak jako podstawa dla szybko rozwijającej się w XIX wieku analizy matematycznej. Dalszym rozszerzeniem pojęcia liczb było opracowanie teorii liczb niewymiernych przez matematyków takich jak Dedekind, Cantor i Weierstrass. Liczby wymierne oraz liczby niewymierne nazywamy łącznie liczbami rzeczywistymi. Między zbiorem liczb rzeczywistych a zbiorem punktów na linii prostej można ustalić jednoznaczną odpowiedniość, co oznacza, że każdej liczbie rzeczywistej odpowiada dokładnie jeden punkt prostej i na odwrót.

Liczby zespolone i dalsze rozszerzenia

Znacznym rozszerzeniem pojęcia liczb było wprowadzenie liczb zespolonych, których szczególnym przypadkiem są liczby rzeczywiste. Liczby zespolone znalazły szerokie zastosowanie w matematyce oraz w naukach przyrodniczych, umożliwiając rozwiązywanie równań, które nie miałyby rozwiązania w zbiorze liczb rzeczywistych.

Warto dodać, że rozwój teorii liczb nie zakończył się na liczbach zespolonych. W matematyce wyższej rozważa się również inne struktury liczbowe, takie jak kwaterniony czy oktawy, które rozszerzają pojęcie liczby jeszcze dalej, choć kosztem niektórych własności algebraicznych znanych z liczb rzeczywistych i zespolonych.

Klasyfikacja liczb

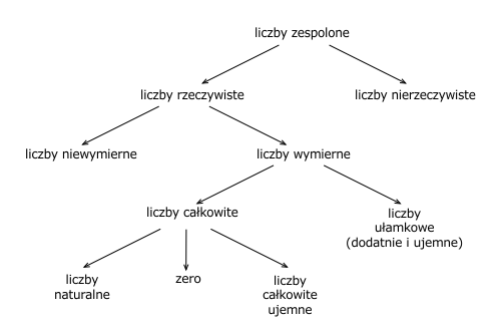
Powyższy diagram ilustruje hierarchię różnych rodzajów liczb, pokazując jak każdy kolejny zbiór zawiera się w następnym, tworząc coraz bogatsze struktury matematyczne.

Podsumowanie

Historia rozwoju pojęcia liczby jest fascynującym odzwierciedleniem ewolucji ludzkiego myślenia matematycznego. Od prostych liczb naturalnych, przez ujemne, wymierne, niewymierne, aż po zespolone i jeszcze bardziej abstrakcyjne konstrukcje, każde rozszerzenie pojęcia liczby otwierało nowe możliwości w matematyce i naukach ścisłych. Zrozumienie tej ewolucji jest kluczowe dla głębszego pojmowania fundamentów matematyki i jej zastosowań w różnych dziedzinach nauki i techniki. Liczby, w swojej różnorodności i bogactwie, pozostają jednym z najważniejszych i najbardziej uniwersalnych narzędzi, jakie ludzkość stworzyła do opisu i zrozumienia otaczającego nas świata.