Okrąg opisany na czworokącie dowolnym

Okrąg opisany na czworokącie dowolnym to okrąg, który przechodzi przez wszystkie cztery wierzchołki tego czworokąta. Oznacza to, że wszystkie wierzchołki czworokąta leżą na okręgu. Taki okrąg nazywany jest również okręgiem opisanym na czworokącie.

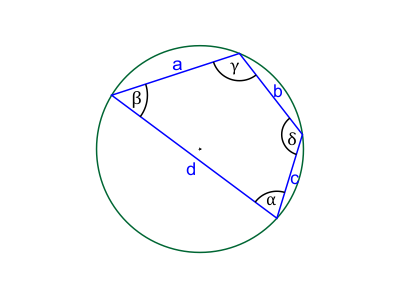
Na powyższym obrazku:

• $a$, $b$, $c$, $d$ – długości boków czworokąta,
• $\alpha$, $\beta$, $\gamma$, $\delta$ – miary kątów wewnętrznych czworokąta.

Warunki istnienia okręgu opisanego na czworokącie

Okrąg można opisać na czworokącie wtedy i tylko wtedy, gdy suma miar przeciwległych kątów czworokąta jest równa $180^\circ$. Oznacza to, że dla dowolnego czworokąta, aby istniał okrąg opisany, muszą być spełnione następujące warunki:

$$\alpha + \gamma = \beta + \delta = 180^\circ$$

Jeśli powyższe równania są spełnione, wówczas czworokąt jest czworokątem opisanym, a jego wierzchołki leżą na jednym okręgu.

Symetralne boków czworokąta

Kolejnym warunkiem na to, aby można było opisać okrąg na czworokącie, jest to, że symetralne wszystkich jego boków muszą przecinać się w jednym punkcie. Ten punkt przecięcia jest jednocześnie środkiem okręgu opisanego. Symetralna boku to prosta prostopadła do tego boku, przechodząca przez jego środek.

W praktyce oznacza to, że jeśli uda nam się znaleźć punkt przecięcia symetralnych boków czworokąta, to będzie to środek okręgu opisanego, a wszystkie wierzchołki czworokąta będą leżały na tym okręgu.

Zastosowania i znaczenie

Znajomość warunków, w których można opisać okrąg na czworokącie, jest przydatna nie tylko w teorii geometrii, ale również w różnych zastosowaniach praktycznych, takich jak projektowanie, inżynieria czy architektura. Okrąg opisany na czworokącie pojawia się również w wielu problemach matematycznych, które wymagają analizy i dowodów geometrycznych.

Podsumowanie

Okrąg można opisać na dowolnym czworokącie, jeśli spełnione są określone warunki dotyczące kątów wewnętrznych oraz symetralnych boków. Zrozumienie tych warunków jest kluczowe dla analizy geometrycznej czworokątów oraz ich właściwości. Dzięki temu można lepiej zrozumieć relacje między elementami czworokąta i zastosować tę wiedzę w praktyce.