Romb
Romb to szczególny rodzaj czworokąta, w którym wszystkie boki mają równą długość. Potocznie romb można opisać jako "pochylony kwadrat". Jest to figura o wyjątkowych właściwościach geometrycznych, łącząca cechy kwadratu i równoległoboku.
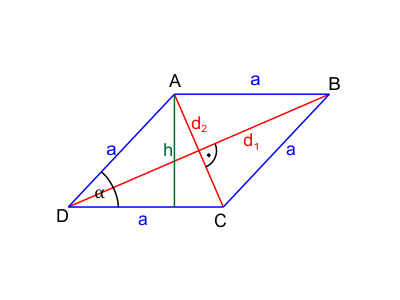
Elementy rombu
Oznaczenia na rysunku:
- $a$ - długość boku rombu
- $d_1$, $d_2$ - długości przekątnych rombu
- $h$ - długość wysokości rombu
- $\alpha$ - miara kąta zawartego pomiędzy dwoma bokami rombu
Bok narysowany poziomo (oznaczony jako $a$) często nazywamy podstawą rombu. Wysokość $h$ jest opuszczona do podstawy $a$ pod kątem prostym (90°).
Właściwości rombu
- Wszystkie boki rombu są równej długości
- Przeciwległe kąty są równe
- Przekątne przecinają się pod kątem prostym
- Przekątne dzielą się wzajemnie na połowy
- Przekątne dzielą romb na cztery przystające trójkąty prostokątne
- Suma miar sąsiednich kątów wewnętrznych wynosi 180°
- Romb posiada dwie osie symetrii przechodzące przez jego przekątne
- Romb jest środkowo symetryczny względem punktu przecięcia przekątnych
Obliczenia związane z rombem
Obwód rombu
Obwód rombu to suma długości wszystkich boków:
$$Obw=4a$$
Pole powierzchni rombu
Pole rombu można obliczyć na kilka sposobów:
- Wykorzystując bok i wysokość:
$$P=ah$$
- Wykorzystując bok i sinus kąta między bokami:
$$P=a^2\sin\alpha$$
- Wykorzystując długości przekątnych:
$$P=\frac{1}{2}d_1d_2$$
Związek rombu z innymi figurami geometrycznymi
Romb jest szczególnym przypadkiem kilku innych figur geometrycznych:
- Romb jest równoległobokiem, w którym wszystkie boki są równej długości
- Kwadrat jest szczególnym przypadkiem rombu, w którym wszystkie kąty są proste (90°)
- Romb jest deltoidem, w którym wszystkie boki są równej długości
Zastosowania rombu
Romb znajduje zastosowanie w wielu dziedzinach:
- Architektura i design: jako element dekoracyjny lub strukturalny
- Inżynieria: w konstrukcjach kratownicowych
- Optyka: w konstrukcji niektórych pryzmatów
- Krystalografia: w opisie struktury kryształów
- Sztuka i wzornictwo: jako motyw w tkaninach, mozaikach i innych formach sztuki
Ciekawostki
- W talii kart symbol karo ma kształt rombu
- Wiele znaków drogowych ma kształt rombu
- W niektórych krajach monety mają kształt rombu
Powiązane zagadnienia
Aby pogłębić zrozumienie własności rombu, warto zapoznać się z następującymi tematami:
Zrozumienie właściwości rombu jest istotne dla dalszego studiowania geometrii i jej praktycznych zastosowań w różnych dziedzinach nauki, techniki i sztuki.