Okrąg opisany na prostokącie
Okrąg opisany na prostokącie to okrąg, który przechodzi przez wszystkie wierzchołki prostokąta. Jest to szczególny przypadek okręgu opisanego na czworokącie, który ma interesujące własności geometryczne.
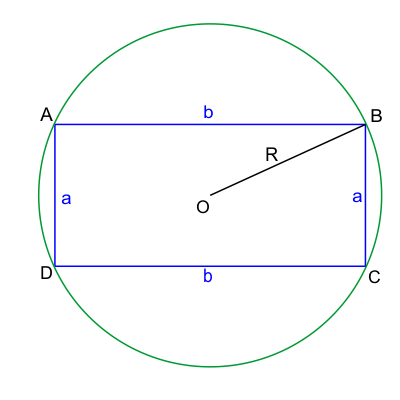
Właściwości okręgu opisanego na prostokącie
- Środek okręgu: Punkt przecięcia się przekątnych prostokąta jest jednocześnie środkiem okręgu opisanego.
- Promień okręgu: Promień okręgu opisanego jest równy połowie długości przekątnej prostokąta.
- Styczne: Boki prostokąta są styczne do okręgu opisanego tylko w wierzchołkach prostokąta.
Wzór na promień okręgu opisanego
Promień okręgu opisanego na prostokącie można obliczyć za pomocą wzoru:
$$R=\frac{1}{2}d$$
gdzie:
$R$ - promień okręgu opisanego,
$d$ - długość przekątnej prostokąta.
Związek z twierdzeniem Pitagorasa
Ponieważ przekątna prostokąta tworzy trójkąt prostokątny z jego bokami, możemy wykorzystać twierdzenie Pitagorasa do obliczenia długości przekątnej:
$$d = \sqrt{a^2 + b^2}$$
gdzie $a$ i $b$ to długości boków prostokąta.
Łącząc to z wzorem na promień, otrzymujemy:
$$R = \frac{1}{2}\sqrt{a^2 + b^2}$$
Okrąg wpisany w prostokąt
Warto zauważyć, że nie ma możliwości wpisania okręgu w prostokąt, chyba że jest to kwadrat. Jest to związane z faktem, że w prostokącie odległości od środka do boków nie są równe, co jest warunkiem koniecznym dla okręgu wpisanego.
Zastosowania praktyczne
Zrozumienie właściwości okręgu opisanego na prostokącie ma zastosowania w różnych dziedzinach:
- Architektura: Projektowanie konstrukcji łączących elementy prostokątne i koliste.
- Inżynieria: Analiza naprężeń w konstrukcjach prostokątnych.
- Grafika komputerowa: Tworzenie algorytmów do rysowania i manipulowania kształtami.
- Optymalizacja: Rozwiązywanie problemów pakowania i rozmieszczania obiektów.
Powiązane zagadnienia
Aby pogłębić zrozumienie tego tematu, warto zapoznać się z następującymi zagadnieniami:
Zrozumienie relacji między prostokątem a okręgiem opisanym pomaga rozwinąć intuicję geometryczną i stanowi podstawę do bardziej zaawansowanych koncepcji w geometrii analitycznej i projektowaniu.