Wykres funkcji wymiernej

Wykresem funkcji wymiernej $y=\frac{a}{x}$, gdzie $a \neq 0$, jest hiperbola równoramienna. Warto podkreślić, że hiperbola ta ma dwie asymptoty, którymi są osie współrzędnych. Funkcja wymierna jest nieciągła w punkcie $x=0$, co oznacza, że jej wykres ma przerwę w tym punkcie, a wartości funkcji dążą do nieskończoności w miarę zbliżania się do tej wartości.

Charakterystyka funkcji dla różnych wartości $a$

Funkcja malejąca dla $a > 0$

Gdy $a > 0$, funkcja jest malejąca w dwóch przedziałach: od $0$ do $-\infty$ w przedziale $(-\infty, 0)$ oraz od $+\infty$ do $0$ w przedziale $(0, +\infty)$. Oznacza to, że wartości funkcji zmniejszają się w miarę oddalania się od osi współrzędnych. Wierzchołki hiperboli znajdują się w punktach $A(\sqrt{a}, \sqrt{a})$ oraz $B(-\sqrt{a}, -\sqrt{a})$, a wykres przecina pierwszą i trzecią ćwiartkę układu współrzędnych.

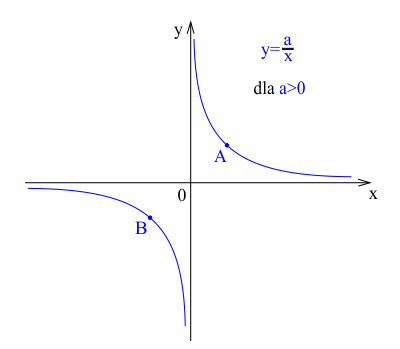
Na wykresie funkcji malejącej można zaobserwować, że krzywa hiperboli nigdy nie przecina osi współrzędnych, lecz zbliża się do nich w miarę oddalania się od początku układu współrzędnych. Takie zachowanie jest związane z obecnością asymptot, które odgrywają kluczową rolę w zrozumieniu zachowania funkcji wymiernych.

Funkcja rosnąca dla $a < 0$

Gdy $a < 0$, funkcja staje się rosnąca, ale w dwóch oddzielnych przedziałach: od $-\infty$ do $0$ w przedziale $(-\infty, 0)$ oraz od $0$ do $+\infty$ w przedziale $(0, +\infty)$. W tym przypadku wierzchołki hiperboli znajdują się w punktach $A'(-\sqrt{|a|}, \sqrt{|a|})$ oraz $B'(\sqrt{|a|}, -\sqrt{|a|})$, a wykres przecina drugą i czwartą ćwiartkę układu współrzędnych.

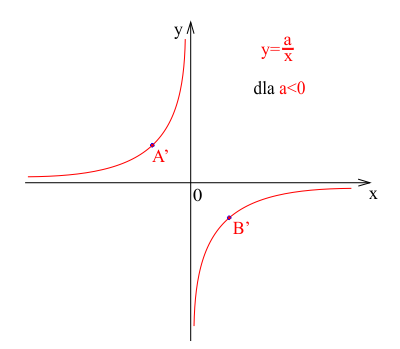
Warto zwrócić uwagę, że choć funkcja ta jest rosnąca, to podobnie jak w przypadku funkcji malejącej, wykres hiperboli zbliża się do osi współrzędnych, ale nigdy ich nie przecina. Taki kształt jest typowy dla funkcji wymiernych i można go spotkać również w innych kontekstach, takich jak analiza funkcji odwrotnych.

Zastosowania i analiza funkcji wymiernych

Funkcje wymierne, takie jak $y = \frac{a}{x}$, mają szerokie zastosowanie w nauce i technice. Przykłady obejmują prawa opisujące zależności odwrotne, takie jak natężenie światła malejące z kwadratem odległości od źródła, czy zależności w obwodach elektrycznych. W analizie matematycznej funkcje te służą do badania zjawisk, gdzie zmienne są związane odwrotnie proporcjonalnie.

Podczas pracy z funkcjami wymiernymi, umiejętność rysowania wykresów oraz zrozumienie ich asymptotycznych właściwości jest kluczowe. Rysowanie wykresów innych typów funkcji, jak na przykład wykresy funkcji logarytmicznej, może również dostarczyć cennych spostrzeżeń na temat zachowania bardziej złożonych funkcji.

Podsumowanie

Funkcje wymierne i ich wykresy są istotnym elementem matematyki, szczególnie w kontekście hiperbol równoramiennych. Dzięki analizie tych funkcji możemy modelować różne zjawiska i lepiej zrozumieć zależności między zmiennymi w kontekście odwrotnej proporcjonalności. Umiejętność pracy z tymi funkcjami jest kluczowa zarówno w matematyce teoretycznej, jak i jej zastosowaniach praktycznych.