Wykres funkcji kwadratowej
Wykresem funkcji kwadratowej jest krzywa zwana parabolą. Parabola jest jedną z podstawowych krzywych w matematyce, o szerokim zastosowaniu w wielu dziedzinach, od fizyki po inżynierię. Kształt paraboli i jej położenie na układzie współrzędnych są ściśle związane z wartościami współczynników funkcji kwadratowej.
Własności paraboli
Ramiona paraboli
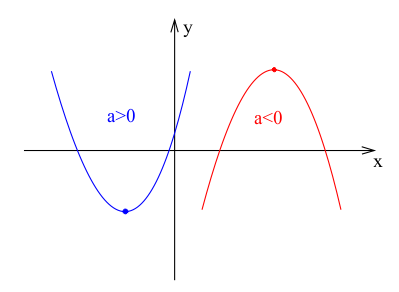
Ramiona paraboli mogą być skierowane w górę lub w dół, w zależności od znaku współczynnika $a$:
- Jeśli współczynnik $a > 0$, ramiona paraboli skierowane są w górę.
- Jeśli współczynnik $a < 0$, ramiona paraboli skierowane są w dół.
- Jeśli współczynnik $a = 0$, funkcja jest funkcją liniową, a wykres jest prostą.
Wierzchołek paraboli
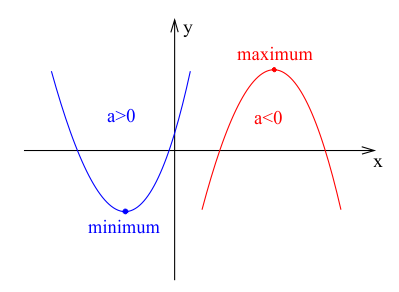
Parabola posiada jeden wierzchołek, który jest punktem ekstremalnym funkcji kwadratowej. Wierzchołek może być minimum lub maksimum funkcji:
- Jeśli współczynnik $a > 0$, w wierzchołku paraboli znajduje się minimum funkcji.
- Jeśli współczynnik $a < 0$, w wierzchołku paraboli znajduje się maksimum funkcji.
Położenie wierzchołka można określić za pomocą wzoru $x = -\frac{b}{2a}$, który wyznacza oś symetrii paraboli. Współrzędne wierzchołka są kluczowe w analizie funkcji kwadratowej, ponieważ determinują zarówno punkt ekstremum, jak i symetrię paraboli.
Miejsca zerowe paraboli
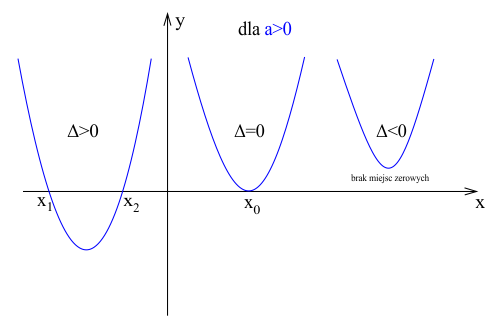
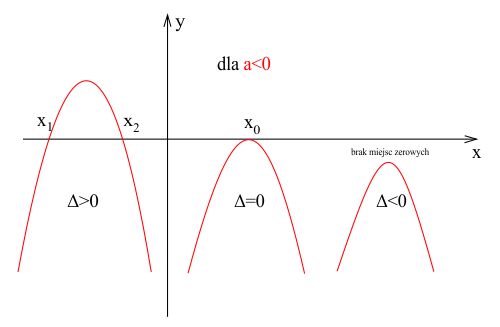
Parabola może przecinać oś X w dwóch miejscach, jednym miejscu lub w ogóle:
- Dla $\Delta > 0$ – parabola przecina oś X w dwóch miejscach.
- Dla $\Delta = 0$ – parabola przecina oś X w jednym miejscu.
- Dla $\Delta < 0$ – parabola nie przecina się z osią X.
Miejsca zerowe są kluczowe w analizie funkcji kwadratowej, ponieważ wskazują punkty, w których funkcja przyjmuje wartość zerową. Obliczanie miejsc zerowych jest często związane z rozwiązywaniem równań kwadratowych, co można uprościć za pomocą postaci iloczynowej funkcji kwadratowej.
Przecięcie się z osią Y
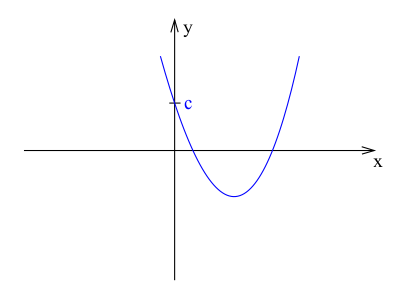
Parabola przecina się z osią Y dokładnie w jednym miejscu, dla wartości $y = c$. Punkt ten jest łatwy do wyznaczenia, ponieważ odpowiada wartości funkcji dla $x = 0$. Wartość $c$ to wyraz wolny funkcji kwadratowej, który decyduje o położeniu punktu przecięcia z osią Y.
Podsumowanie
Wykres funkcji kwadratowej, czyli parabola, posiada wiele unikalnych właściwości, które są bezpośrednio związane z wartościami współczynników funkcji. Rozumienie tych właściwości jest kluczowe dla pełnej analizy funkcji kwadratowej, a także dla rozwiązywania zadań matematycznych związanych z tym typem funkcji. Parabola znajduje zastosowanie w różnych dziedzinach nauki i techniki, od modelowania ruchu ciał po analizę danych w statystyce.