Okrąg wpisany i opisany na kwadracie

Kwadrat jest szczególną figurą geometryczną, w której można zarówno wpisać okrąg, jak i opisać okrąg na zewnątrz. Okrąg wpisany styka się ze wszystkimi bokami kwadratu, natomiast okrąg opisany przechodzi przez wszystkie wierzchołki kwadratu.

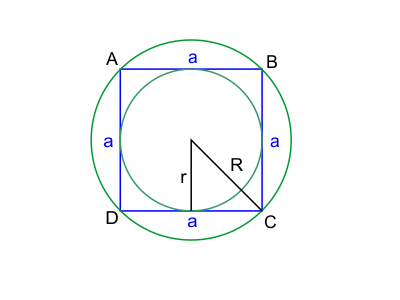
Okrąg wpisany w kwadrat

Okrąg wpisany to taki, który jest styczny do wszystkich boków kwadratu od wewnątrz. Środek tego okręgu pokrywa się ze środkiem kwadratu.

Długość promienia $r$ okręgu wpisanego w kwadrat można łatwo obliczyć, ponieważ równa jest ona połowie długości boku kwadratu $a$:

$$r = \frac{1}{2}a$$

Innymi słowy, promień okręgu wpisanego jest połową długości boku kwadratu.

Okrąg opisany na kwadracie

Okrąg opisany na kwadracie to taki, który przechodzi przez wszystkie jego wierzchołki. Również w tym przypadku środek okręgu pokrywa się ze środkiem kwadratu.

Długość promienia $R$ okręgu opisanego równa jest połowie długości przekątnej kwadratu. Przekątną $d$ kwadratu można obliczyć przy użyciu twierdzenia Pitagorasa:

$$d = a\sqrt{2}$$

W związku z tym długość promienia $R$ okręgu opisanego wynosi:

$$R = \frac{1}{2}d = \frac{1}{2}a\sqrt{2} = \frac{a\sqrt{2}}{2}$$

Promień okręgu opisanego jest zatem równy połowie długości przekątnej kwadratu, co można wyrazić jako $R = \frac{a\sqrt{2}}{2}$.

Podsumowanie

Podsumowując, promień okręgu wpisanego w kwadrat to połowa długości boku kwadratu, natomiast promień okręgu opisanego na kwadracie to połowa długości przekątnej tego kwadratu. Obie te zależności wynikają bezpośrednio z geometrycznych właściwości kwadratu.