Równoległobok
Równoległobok to czworokąt posiadający dwie pary równoległych boków. Boki równoległe do siebie mają identyczną długość. Potocznie równoległobok można opisać jako "pochylony prostokąt".
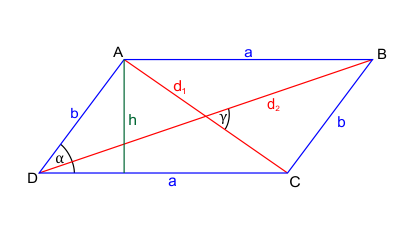
Elementy równoległoboku
Oznaczenia na rysunku:
- $a$, $b$ - długości boków równoległoboku
- $d_1$, $d_2$ - długości przekątnych równoległoboku
- $h$ - długość wysokości równoległoboku
- $\alpha$ - miara kąta zawartego pomiędzy dwoma bokami równoległoboku
- $\gamma$ - miara kąta pod jakim przecinają się przekątne równoległoboku
Bok narysowany poziomo (oznaczony jako $a$) często nazywamy podstawą równoległoboku. Wysokość $h$ jest opuszczona do podstawy $a$ pod kątem prostym (90°).
Właściwości równoległoboku
- Przeciwległe boki są równoległe i równej długości
- Przeciwległe kąty są równe
- Przekątne przecinają się w połowie swojej długości
- Suma miar sąsiednich kątów wewnętrznych wynosi 180°
- Równoległobok jest środkowo symetryczny względem punktu przecięcia przekątnych
Obliczenia związane z równoległobokiem
Obwód równoległoboku
Obwód równoległoboku to suma długości wszystkich boków:
$$Obw=2a+2b=2(a+b)$$
Pole powierzchni równoległoboku
Pole równoległoboku można obliczyć na kilka sposobów:
- Wykorzystując podstawę i wysokość:
$$P=ah$$
- Wykorzystując długości boków i kąt między nimi:
$$P=ab\sin\alpha$$
- Wykorzystując długości przekątnych i kąt między nimi:
$$P=\frac{1}{2}d_1d_2\sin\gamma$$
Szczególne przypadki równoległoboku
Równoległobok obejmuje kilka szczególnych przypadków:
- Romb - równoległobok o wszystkich bokach równych ($a=b$)
- Prostokąt - równoległobok o wszystkich kątach prostych
- Kwadrat - równoległobok o wszystkich bokach równych i wszystkich kątach prostych
Warto zauważyć, że równoległobok jest szczególnym przypadkiem trapezu.
Okrąg a równoległobok
W przeciwieństwie do niektórych innych czworokątów:
- Na równoległoboku nie można opisać okręgu (z wyjątkiem przypadku, gdy jest to prostokąt)
- W równoległobok nie można wpisać okręgu (z wyjątkiem przypadku, gdy jest to kwadrat)
Zastosowania równoległoboku
Równoległoboki mają wiele zastosowań praktycznych:
- W architekturze i designie, jako elementy konstrukcyjne lub dekoracyjne
- W mechanice, przy projektowaniu układów przenoszenia ruchu
- W grafice komputerowej, jako podstawowe kształty w programach do projektowania
- W optyce, przy analizie odbić światła
Powiązane zagadnienia
Aby pogłębić zrozumienie własności równoległoboku, warto zapoznać się z następującymi tematami:
Zrozumienie właściwości równoległoboku jest kluczowe dla dalszego studiowania geometrii i jej praktycznych zastosowań w różnych dziedzinach nauki i techniki.