Wykres wartości bezwzględnej

Funkcja wartości bezwzględnej $f(x) = |x|$ jest jedną z podstawowych funkcji w matematyce, której wykres ma charakterystyczny kształt litery "V".

Definicja i kształt wykresu

Wartość bezwzględna z liczby dodatniej jest równa tej samej liczbie, więc wykresem funkcji dla argumentów większych od zera ($x > 0$) będzie funkcja liniowa $f(x) = x$. Natomiast dla argumentów mniejszych od zera ($x < 0$), wartość bezwzględna zmienia znak liczby na dodatni, więc wykresem funkcji będzie funkcja liniowa $f(x) = -x$. W rezultacie wykres funkcji $f(x) = |x|$ składa się z dwóch odcinków linii prostych, które przecinają się w punkcie $(0,0)$.

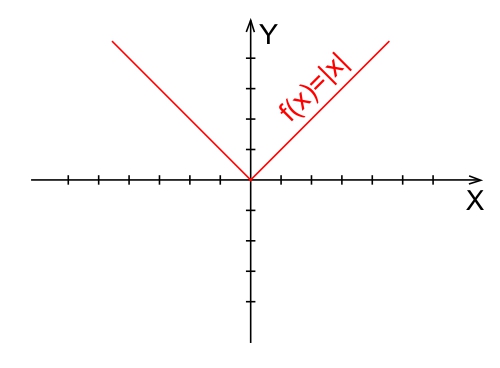
Właściwości wykresu

• Dla $x \ge 0$, funkcja jest linią prostą o nachyleniu 1, czyli $f(x) = x$.
• Dla $x < 0$, funkcja jest linią prostą o nachyleniu -1, czyli $f(x) = -x$.
• Punkt $(0,0)$ jest wierzchołkiem wykresu i jednocześnie punktem, w którym funkcja nie jest różniczkowalna.
• Wykres jest symetryczny względem osi Y.
• Funkcja jest ciągła w każdym punkcie, ale nie jest różniczkowalna w punkcie $x = 0$.

Transformacje wykresu funkcji wartości bezwzględnej

Wykres funkcji wartości bezwzględnej może być poddany różnym transformacjom:

1. Przesunięcie poziome

$f(x) = |x - a|$ przesuwa wykres o $a$ jednostek w prawo.

2. Przesunięcie pionowe

$f(x) = |x| + b$ przesuwa wykres o $b$ jednostek w górę.

3. Rozciągnięcie/zwężenie pionowe

$f(x) = c|x|$, gdzie $c > 0$, rozciąga wykres pionowo dla $c > 1$ lub zwęża dla $0 < c < 1$.

4. Odbicie względem osi X

$f(x) = -|x|$ odwraca wykres "do góry nogami".

Zastosowania wykresu wartości bezwzględnej

Wykres funkcji wartości bezwzględnej jest używany w wielu dziedzinach matematyki i nauki:

• Geometria Do wizualizacji odległości punktów od zera na osi liczbowej.
• Analiza matematyczna Przy rozwiązywaniu równań i nierówności zawierających wartość bezwzględną.
• Fizyka: Do modelowania wielkości fizycznych, które są zawsze dodatnie, takich jak prędkość czy energia.
• Informatyka: W algorytmach i obliczeniach, gdzie konieczne jest uwzględnienie absolutnych wartości danych liczbowych.
• Ekonomia: W modelowaniu kosztów i zysków, gdzie istotne są wartości bezwzględne.

Równania i nierówności z wartością bezwzględną

Wykres funkcji wartości bezwzględnej jest szczególnie przydatny przy rozwiązywaniu równań i nierówności:

Równanie $|x| = a$ (dla $a \ge 0$)

Rozwiązanie: $x = a$ lub $x = -a$

Nierówność $|x| < a$ (dla $a > 0$)

Rozwiązanie: $-a < x < a$

Nierówność $|x| > a$ (dla $a \ge 0$)

Rozwiązanie: $x < -a$ lub $x > a$

Podsumowanie

Wykres funkcji wartości bezwzględnej, ze swoim charakterystycznym kształtem litery "V", jest fundamentalnym elementem w zrozumieniu wielu koncepcji matematycznych. Jego właściwości, takie jak symetria względem osi Y i brak różniczkowalności w punkcie $(0,0)$, czynią go unikalnym i ważnym narzędziem w analizie matematycznej. Znajomość tego wykresu i jego transformacji jest kluczowa dla rozwiązywania równań i nierówności zawierających wartość bezwzględną, a także dla modelowania zjawisk w fizyce i ekonomii.