Twierdzenie Pitagorasa
Twierdzenie Pitagorasa jest jednym z najważniejszych twierdzeń w geometrii, szczególnie związanym z trójkątem prostokątnym. Jest to fundamentalne twierdzenie, które ma szerokie zastosowanie w różnych dziedzinach nauki i techniki.
W trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej.
Twierdzenie Pitagorasa można zapisać w postaci wzoru:
$$a^2 + b^2 = c^2$$
Gdzie:
- $a$ i $b$ – długości przyprostokątnych,
- $c$ – długość przeciwprostokątnej.
Ilustracja graficzna Twierdzenia Pitagorasa wygląda następująco:
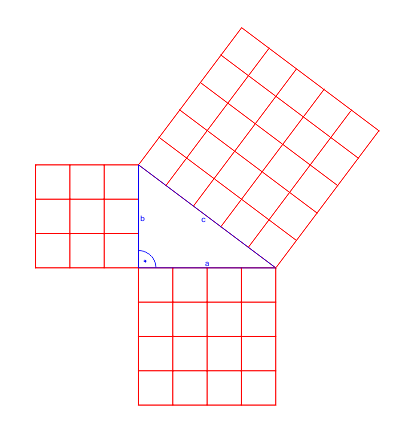
Zastosowania Twierdzenia Pitagorasa
Twierdzenie Pitagorasa znajduje zastosowanie w wielu dziedzinach matematyki i nauk ścisłych:
- Geometria: Używane do obliczania długości boków trójkąta prostokątnego oraz w rozwiązywaniu zadań związanych z trójkątami.
- Trygonometria: Stanowi podstawę do wyprowadzenia funkcji trygonometrycznych.
- Fizyka: Wykorzystywane do obliczania wielkości wektorowych, takich jak siły czy prędkości.
- Architektura i budownictwo: Stosowane przy projektowaniu i analizie konstrukcji budowlanych.
- Nawigacja: Używane do obliczania odległości między punktami w przestrzeni.
Trójkąty pitagorejskie
Trójkąty pitagorejskie to trójkąty prostokątne, których boki mają długości wyrażone liczbami całkowitymi. Takie trójkąty są często wykorzystywane w praktyce ze względu na ich proste zależności liczbowe.
Najmniejszy trójkąt pitagorejski ma boki o długościach $3$, $4$, $5$. Sprawdzenie, że spełnia on Twierdzenie Pitagorasa:
$$3^2 + 4^2 = 5^2$$
$$9 + 16 = 25$$
Inne przykłady trójkątów pitagorejskich to:
- $(5, 12, 13)$,
- $(8, 15, 17)$,
- $(7, 24, 25)$.
Dowód Twierdzenia Pitagorasa
Istnieje wiele sposobów dowodzenia Twierdzenia Pitagorasa, ale jednym z najprostszych jest dowód oparty na podobieństwie trójkątów:
- Narysuj wysokość z wierzchołka kąta prostego na przeciwprostokątną.
- Powstałe dwa trójkąty są podobne do siebie i do trójkąta początkowego.
- Z podobieństwa tych trójkątów wynikają proporcje, które prowadzą bezpośrednio do Twierdzenia Pitagorasa.
Twierdzenie Pitagorasa stanowi podstawę wielu innych twierdzeń w geometrii i jest kluczowe dla zrozumienia geometrii euklidesowej.
Podsumowanie
Twierdzenie Pitagorasa jest nie tylko jednym z najbardziej rozpoznawalnych twierdzeń w matematyce, ale także narzędziem o szerokim zastosowaniu praktycznym. Jego znajomość jest niezbędna w wielu dziedzinach nauki i techniki, od podstawowej geometrii po zaawansowane analizy w fizyce i inżynierii.