Pierwiastkowanie liczb zespolonych

Wyciąganie pierwiastka stopnia $n$ z liczby zespolonej jest operacją odwrotną do potęgowania i wykorzystuje wzór de Moivre'a dla wykładników ułamkowych. Jeśli liczba zespolona $z$ jest wyrażona w postaci trygonometrycznej jako:

$$ z = |z|(\cos \varphi + i\sin \varphi) $$

oraz $n$ jest liczbą naturalną, to pierwiastek stopnia $n$ z liczby zespolonej $z$ jest dany wzorem:

$$ \sqrt[n]{z} = \sqrt[n]{|z|}\left(\cos \frac{\varphi + 2k\pi}{n} + i\sin \frac{\varphi + 2k\pi}{n}\right) $$

gdzie $k = 0, 1, 2, \ldots, n-1$. Każda z tych wartości odpowiada innemu pierwiastkowi z liczby zespolonej.

Jednoznaczność i wieloznaczność pierwiastków

Operacje takie jak dodawanie, odejmowanie, mnożenie, dzielenie oraz potęgowanie liczb zespolonych dla wykładników całkowitych są jednoznaczne. Oznacza to, że dla każdej pary liczb zespolonych istnieje dokładnie jeden wynik tych operacji.

Natomiast wyciąganie pierwiastka stopnia $n$ z liczby zespolonej jest operacją wieloznaczną. Dla dowolnej liczby naturalnej $n$, istnieje dokładnie $n$ różnych wartości pierwiastka $n$-tego stopnia z liczby zespolonej. Wynika to z faktu, że funkcje trygonometryczne są okresowe i dla każdego $k = 0, 1, 2, \ldots, n-1$, wartość pierwiastka jest inna.

Wyniki te różnią się argumentami, które dla pierwiastka $n$-tego stopnia przyjmują wartości:

$$ \frac{\varphi}{n}, \quad \frac{\varphi + 2\pi}{n}, \quad \frac{\varphi + 4\pi}{n}, \quad \ldots, \quad \frac{\varphi + 2(n-1)\pi}{n} $$

Wartości te są równomiernie rozłożone na okręgu jednostkowym i różnią się o kąt $\frac{2\pi}{n}$. Po wykorzystaniu wszystkich $n$ wartości $k$, kolejne wartości pierwiastków zaczynają się powtarzać cyklicznie.

Interpretacja geometryczna

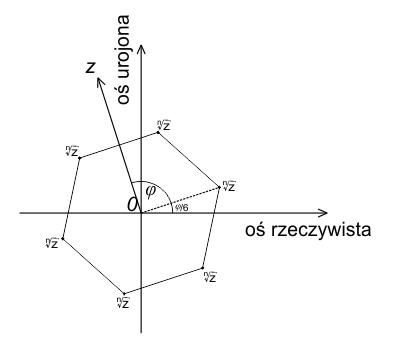
Geometria wyciągania pierwiastka stopnia $n$ z liczby zespolonej jest bardzo intuicyjna. Wszystkie $n$ pierwiastków są równomiernie rozmieszczone na okręgu o promieniu równym $\sqrt[n]{|z|}$ i są wierzchołkami wielokąta foremnego o $n$ bokach, którego środek znajduje się w początku układu współrzędnych (biegunie).

Na poniższym rysunku przedstawiono sześć wartości pierwiastka szóstego stopnia z liczby zespolonej. Każdy z pierwiastków jest jednym z wierzchołków sześciokąta foremnego na płaszczyźnie zespolonej.

Przykład wyciągania pierwiastków

Rozważmy przykład wyciągania pierwiastka trzeciego stopnia z liczby zespolonej $z = 8(\cos \frac{\pi}{3} + i\sin \frac{\pi}{3})$. Obliczmy trzy pierwiastki trzeciego stopnia z tej liczby:

• Dla $k = 0$: $$ \sqrt[3]{z} = \sqrt[3]{8}\left(\cos \frac{\frac{\pi}{3} + 2 \cdot 0 \cdot \pi}{3} + i\sin \frac{\frac{\pi}{3} + 2 \cdot 0 \cdot \pi}{3}\right) = 2\left(\cos \frac{\pi}{9} + i\sin \frac{\pi}{9}\right) $$
• Dla $k = 1$: $$ \sqrt[3]{z} = 2\left(\cos \frac{\frac{\pi}{3} + 2 \cdot \pi}{3} + i\sin \frac{\frac{\pi}{3} + 2 \cdot \pi}{3}\right) = 2\left(\cos \frac{7\pi}{9} + i\sin \frac{7\pi}{9}\right) $$
• Dla $k = 2$: $$ \sqrt[3]{z} = 2\left(\cos \frac{\frac{\pi}{3} + 4 \cdot \pi}{3} + i\sin \frac{\frac{\pi}{3} + 4 \cdot \pi}{3}\right) = 2\left(\cos \frac{13\pi}{9} + i\sin \frac{13\pi}{9}\right) $$

Podsumowanie

Wyciąganie pierwiastka stopnia $n$ z liczby zespolonej za pomocą wzoru de Moivre'a jest operacją, która daje $n$ różnych wyników, rozłożonych równomiernie na okręgu jednostkowym na płaszczyźnie zespolonej. Każdy z tych wyników jest jednym z wierzchołków wielokąta foremnego, co ma istotne znaczenie w geometrii zespolonej i analizie matematycznej.