Wykres funkcji homograficznej
Funkcja homograficzna, wyrażona wzorem:
$$y = \frac{a_1x + b_1}{a_2x + b_2},$$gdzie $a_2 \neq 0$, jest szczególnym przypadkiem funkcji wymiernej. Wykresem tej funkcji jest hiperbola równoramienna, której asymptoty są równoległe do osi współrzędnych. Asymptoty te mają równania:
- asymptota pozioma: $y = \frac{a_1}{a_2}$,
- asymptota pionowa: $x = -\frac{b_2}{a_2}$.
Asymptoty przecinają się w punkcie $C\left(-\frac{b_2}{a_2}, \frac{a_1}{a_2}\right)$, który jest punktem przecięcia osi symetrii hiperboli.
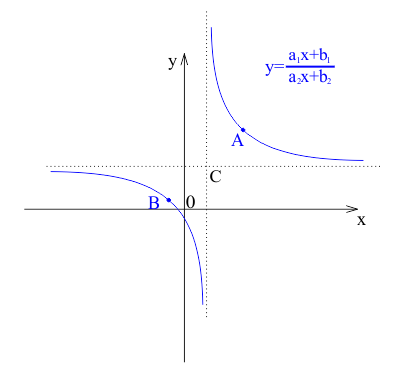
Charakterystyka wykresu funkcji homograficznej
Funkcja homograficzna charakteryzuje się tym, że jej wykres składa się z dwóch gałęzi hiperboli. W zależności od wartości współczynników $a_1$, $b_1$, $a_2$ i $b_2$, wykres może przyjmować różne położenia i kształty. Kluczowe właściwości wykresu obejmują:
- Asymptoty: Linie, do których hiperbola zbliża się, ale nigdy ich nie przecina. Asymptoty funkcji homograficznej są równoległe do osi układu współrzędnych, co różni ten typ hiperboli od ogólnego przypadku funkcji wymiernej, której asymptoty mogą być nachylone pod dowolnym kątem.
- Symetria: Wykres funkcji homograficznej jest symetryczny względem punktu przecięcia asymptot $C\left(-\frac{b_2}{a_2}, \frac{a_1}{a_2}\right)$. Punkt ten stanowi centrum symetrii hiperboli.
- Nieciągłość: Funkcja homograficzna jest nieciągła w punkcie, gdzie mianownik wyrażenia $a_2x + b_2$ przyjmuje wartość zero, co powoduje, że funkcja dąży do nieskończoności w tym punkcie. Wartość ta wyznacza miejsce asymptoty pionowej.
Rysowanie wykresu funkcji homograficznej
Aby narysować wykres funkcji homograficznej, należy wykonać następujące kroki:
- Znajdź asymptoty: Oblicz równania asymptot na podstawie wzoru funkcji. Asymptota pozioma ma równanie $y = \frac{a_1}{a_2}$, a asymptota pionowa $x = -\frac{b_2}{a_2}$.
- Wyznacz punkt przecięcia asymptot: Punkt przecięcia asymptot $C\left(-\frac{b_2}{a_2}, \frac{a_1}{a_2}\right)$ stanowi centrum symetrii wykresu.
- Narysuj hiperbolę: Mając już asymptoty i centrum symetrii, możesz narysować wykres hiperboli, który zbliża się do asymptot, ale ich nie przecina.
Przykładami funkcji homograficznych, których wykresy są hiperbolami równoramiennymi, mogą być również funkcje odwrotne o zmienionych parametrach. .
Zastosowania funkcji homograficznej
Funkcje homograficzne mają wiele zastosowań w różnych dziedzinach matematyki i nauk ścisłych. Przykładowo, są używane w optyce do opisu zjawisk załamania światła oraz w teorii sterowania, gdzie modelują zależności między wielkościami fizycznymi. Funkcje te są również ważne w analizie ekonomicznej, gdzie opisują pewne typy zależności popytu i podaży.
Podsumowanie
Funkcja homograficzna jest ważnym przykładem funkcji wymiernej, której wykres przyjmuje postać hiperboli równoramiennej. Zrozumienie jej właściwości, takich jak asymptoty i symetria, jest kluczowe w analizie wielu zjawisk matematycznych i fizycznych. Dzięki temu możemy lepiej modelować i przewidywać zachowanie różnych systemów, które opisują funkcje homograficzne.