Kwadrat
Kwadrat to czworokąt foremny, który charakteryzuje się wszystkimi bokami równymi oraz kątami wewnętrznymi o mierze 90 stopni. Każdy kwadrat jest szczególnym przypadkiem prostokąta, w którym wszystkie boki są równe.
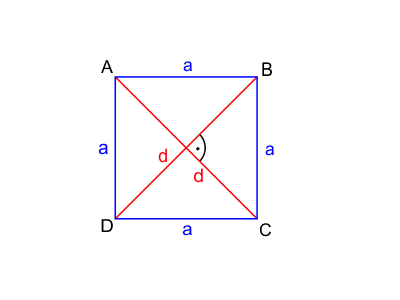
W kwadracie:
- $A$, $B$, $C$, $D$ – wierzchołki kwadratu,
- $a$ – długość boku kwadratu,
- $d$ – długość przekątnej kwadratu.
Właściwości kwadratu
Kwadrat posiada kilka kluczowych właściwości:
- Równe boki: Wszystkie boki kwadratu mają jednakową długość $a$.
- Równe kąty: Wszystkie kąty wewnętrzne kwadratu są kątami prostymi, czyli mają miarę 90 stopni.
- Przekątne: Przekątne kwadratu są równej długości, przecinają się w środku kwadratu pod kątem prostym i dzielą się na połowy. Przekątne kwadratu można obliczyć za pomocą twierdzenia Pitagorasa.
Obwód kwadratu
Obwód kwadratu to suma długości wszystkich jego boków. Możemy go obliczyć za pomocą wzoru:
$$Obw = 4a$$
gdzie $a$ to długość jednego boku kwadratu.
Pole kwadratu
Pole powierzchni kwadratu możemy obliczyć na kilka sposobów:
- Z długości boku:
- Z długości przekątnej:
- Alternatywnie, za pomocą boku i przekątnej:
$$P = a^2$$
$$P = \frac{1}{2}d^2$$
$$P = \frac{\sqrt{2}}{2}ad$$
Długość przekątnej kwadratu
Długość przekątnej kwadratu możemy obliczyć za pomocą twierdzenia Pitagorasa. Przekątna kwadratu tworzy trójkąt prostokątny z dwoma bokami kwadratu jako przyprostokątnymi. Wzór na długość przekątnej to:
$$d = a\sqrt{2}$$
Wynika to z twierdzenia Pitagorasa, gdzie $a$ to długość boku kwadratu.
Podsumowanie
Kwadrat jest jedną z podstawowych figur geometrycznych, z której wynika wiele ważnych własności i zależności. Zrozumienie obliczeń związanych z kwadratem, takich jak obwód, pole i długość przekątnej, jest kluczowe dla dalszej nauki geometrii i innych dziedzin matematyki.