Kąt ostry, prosty, rozwarty, półpełny i pełny
Klasyfikacja kątów według miary
W geometrii, kąty klasyfikujemy według ich miary, co ma kluczowe znaczenie w różnych obliczeniach i konstrukcjach geometrycznych. Poznanie tych podstawowych rodzajów kątów jest niezbędne do zrozumienia bardziej zaawansowanych koncepcji w trygonometrii i geometrii analitycznej.
Kąt ostry
Kąt ostry jest to kąt o mierze większej od $0^\circ$ i jednocześnie mniejszej od $90^\circ$: $\alpha\in(0^\circ;90^\circ)$.
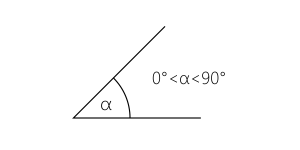
Kąty ostre często występują w trójkątach prostokątnych, gdzie dwa z trzech kątów są zawsze ostre. Są również kluczowe w definicjach funkcji trygonometrycznych.
Kąt prosty
Kąt prosty jest to kąt o mierze równej $90^\circ$: $\alpha = 90^\circ$.
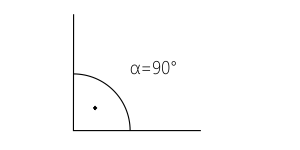
Kąt prosty jest fundamentalny w geometrii. Tworzy go prostopadłość dwóch prostych. Jest podstawą definicji trójkąta prostokątnego i występuje w wielu figurach geometrycznych, takich jak kwadraty czy prostokąty.
Kąt rozwarty
Kąt rozwarty jest to kąt o mierze większej od $90^\circ$ i jednocześnie mniejszej od $180^\circ$: $\alpha\in(90^\circ;180^\circ)$.
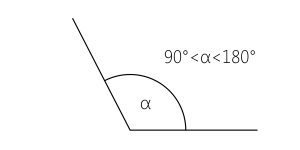
Kąty rozwarte występują w wielu wielokątach, na przykład w trójkątach rozwartokątnych. Mają szczególne znaczenie w trygonometrii, gdzie funkcje dla kątów rozwartych mają inne własności niż dla kątów ostrych.
Kąt półpełny
Kąt półpełny jest to kąt o mierze równej $180^\circ$: $\alpha = 180^\circ$. Oba ramiona kąta tworzą linię prostą.
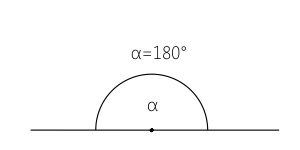
Kąt półpełny jest istotny w geometrii płaskiej. Suma kątów wewnętrznych w trójkącie zawsze wynosi 180°. Kąt półpełny jest też kluczowy w definicji kątów przyległych.
Kąt pełny
Kąt pełny jest to kąt o mierze równej $360^\circ$: $\alpha = 360^\circ$. Oba ramiona kąta pokrywają się ze sobą.
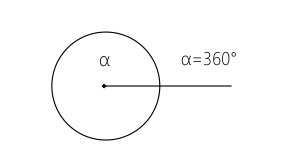
Kąt pełny odpowiada pełnemu obrotowi. Jest ważny w trygonometrii i analizie matematycznej, gdzie funkcje trygonometryczne wykazują okresowość co 360°.
Mierzenie kątów
Kąty można mierzyć za pomocą różnych narzędzi:
- Kątomierz: Najpopularniejsze narzędzie do mierzenia kątów w stopniach.
- Ekierka: Przydatna do szybkiego rozpoznawania kątów 30°, 45°, 60° i 90°.
- Cyrkiel: Można go użyć do przenoszenia i porównywania kątów.
W matematyce wyższej i fizyce często używa się też radianów jako jednostki miary kąta, gdzie pełny obrót odpowiada $2\pi$ radianów.
Zrozumienie różnych rodzajów kątów i umiejętność ich rozpoznawania jest fundamentem dla dalszych studiów geometrii, trygonometrii i wielu dziedzin nauki stosowanej.