Definicja funkcji

Funkcja jest pojęciem często spotykanym w matematyce. Dzięki funkcjom możliwe jest opisanie otaczającego nas świata oraz badanie zjawisk, jakie w nim zachodzą. Funkcję definiuje się jako przyporządkowanie każdemu elementowi zbioru pierwszego dokładnie jednego elementu zbioru drugiego.

Funkcja $f: X \to Y$ to przyporządkowanie, które każdemu elementowi zbioru $X$ przyporządkowuje dokładnie jeden element zbioru $Y$.

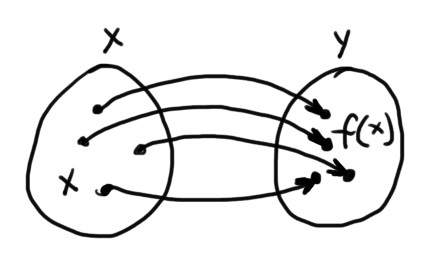
Elementy należące do zbioru $X$ nazywamy argumentami lub dziedziną funkcji. Natomiast elementy zbioru $Y$ to wartości funkcji, a zbiór tych wartości nazywamy przeciwdziedziną.

Reprezentacje funkcji

Funkcję najczęściej przedstawia się za pomocą wzoru lub wykresu. Każda z tych metod ma swoje zalety i może być używana w zależności od kontekstu i celu analizy.

Wzory funkcji

Wzory funkcji są precyzyjnym sposobem ich przedstawienia. Pozwalają one na łatwe przeprowadzenie obliczeń oraz analizę właściwości funkcji, takich jak miejsca zerowe, ekstrema czy asymptoty.

Przykłady wzorów funkcji:

$$f(x) = x^2 + 3x - 8$$

$$y = 4x - 7$$

$$f(x) = \sin x$$

Wykresy funkcji

Wykresy funkcji pozwalają na wizualne przedstawienie zależności między argumentami a wartościami funkcji. Są one szczególnie przydatne do intuicyjnego zrozumienia zachowania funkcji na danym przedziale.

Przykłady wykresów funkcji mogą obejmować:

• Wykresy funkcji liniowych, takich jak $y = 2x + 1$
• Wykresy funkcji kwadratowych, takich jak $f(x) = x^2 - 4x + 4$
• Wykresy funkcji trygonometrycznych, takich jak $f(x) = \cos x$

Podsumowanie

Funkcje są fundamentem matematyki i nauk ścisłych. Pozwalają one na formalne i precyzyjne opisywanie oraz analizowanie różnorodnych zjawisk i procesów. Dzięki różnym sposobom przedstawiania funkcji, takim jak wzory i wykresy, można efektywnie badać ich właściwości oraz zastosowania w praktyce.