Wykres funkcji wykładniczej

Wykresem funkcji wykładniczej jest krzywa wykładnicza. Charakteryzuje się ona kilkoma kluczowymi właściwościami:

• Funkcja wykładnicza przyjmuje tylko wartości dodatnie
• Wykres zawsze przechodzi przez punkt (0, 1)
• Posiada asymptotę poziomą y = 0 (oś OX) dla x → -∞
• Nie posiada miejsc zerowych
• Dziedzina funkcji to cały zbiór liczb rzeczywistych (ℝ)
• Zbiór wartości to zbiór liczb rzeczywistych dodatnich (ℝ⁺)

Wykres funkcji wykładniczej rosnącej (a > 1)

Dla $a > 1$ funkcja wykładnicza jest rosnąca. Oznacza to, że wraz ze wzrostem wartości x, wartość funkcji również rośnie, i to w tempie szybszym niż liniowe.

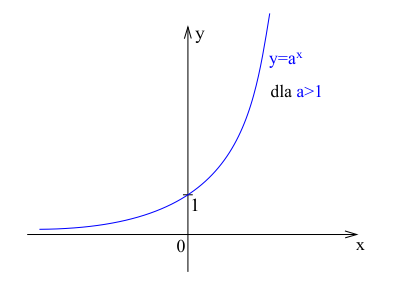
Charakterystyczne cechy wykresu funkcji wykładniczej rosnącej:

• Krzywa "wygięta" do góry
• Dla x < 0, wartości funkcji zbliżają się do 0, ale nigdy go nie osiągają
• Dla x > 0, wartości funkcji rosną coraz szybciej

Wykres funkcji wykładniczej malejącej (0 < a < 1)

Dla $0 < a < 1$ funkcja wykładnicza jest malejąca. W tym przypadku, wraz ze wzrostem wartości x, wartość funkcji maleje.

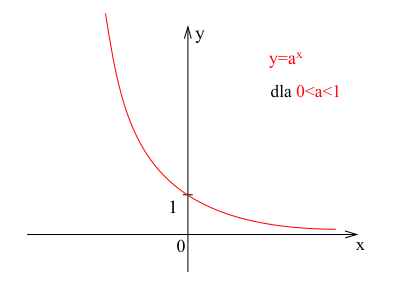
Charakterystyczne cechy wykresu funkcji wykładniczej malejącej:

• Krzywa "wygięta" do dołu
• Dla x < 0, wartości funkcji rosną, zbliżając się do +∞
• Dla x > 0, wartości funkcji zbliżają się do 0, ale nigdy go nie osiągają

Porównanie wykresów

Niezależnie od wartości podstawy a (dla a ≠ 1), wszystkie wykresy funkcji wykładniczych mają pewne wspólne cechy:

• Przechodzą przez punkt (0, 1)
• Nie przecinają osi OX (brak miejsc zerowych)
• Mają asymptotę poziomą y = 0
• Są funkcjami ciągłymi w całej dziedzinie

Zrozumienie kształtu i właściwości wykresu funkcji wykładniczej jest kluczowe dla analizy wielu zjawisk w naukach przyrodniczych i ekonomii, gdzie występuje wzrost wykładniczy lub zanik wykładniczy.