Ostrosłupy

Ostrosłupem nazywamy taki wielościan, którego jedna ze ścian, zwana podstawą ostrosłupa, jest dowolnym wielokątem, natomiast pozostałe ściany, zwane bocznymi ścianami ostrosłupa, zbiegają się w jednym punkcie zwanym wierzchołkiem ostrosłupa. Ściany boczne ostrosłupa są zawsze trójkątami. Gdy podstawą ostrosłupa jest wielokąt foremny, taki ostrosłup nazywamy ostrosłupem prawidłowym.

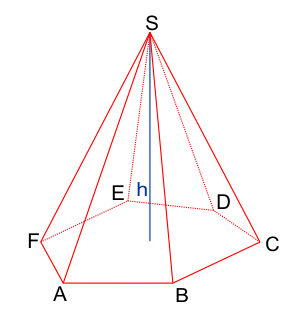
Pole powierzchni ostrosłupa

Pole powierzchni ostrosłupa to suma pól ścian bocznych i pola podstawy. Możemy je wyrazić wzorem:

$$ P = P_b + P_p $$

gdzie:

• $P_b$ – suma wszystkich pól ścian bocznych ostrosłupa,
• $P_p$ – pole podstawy ostrosłupa.

Objętość ostrosłupa

Objętość ostrosłupa można obliczyć jako jedną trzecią iloczynu pola podstawy i wysokości ostrosłupa. Wzór na objętość wygląda następująco:

$$ V = \frac{1}{3}P_p \cdot h $$

gdzie:

• $P_p$ – pole podstawy ostrosłupa,
• $h$ – wysokość ostrosłupa, czyli odległość od wierzchołka do płaszczyzny podstawy.

Przykład zastosowania wzorów

Rozważmy ostrosłup o podstawie kwadratu, którego bok ma długość $a$, oraz wysokości $h$. Pole podstawy $P_p$ to pole kwadratu, które wynosi $a^2$. Aby obliczyć pole powierzchni całkowitej ostrosłupa, należy znać również pola ścian bocznych, które w tym przypadku są trójkątami równoramiennymi.

Objętość takiego ostrosłupa można wyrazić wzorem:

$$ V = \frac{1}{3}a^2 \cdot h $$

Warto zauważyć, że ostrosłupy są powszechnie spotykane w architekturze i sztuce, gdzie często stosuje się je jako elementy dekoracyjne oraz konstrukcyjne.