Interpretacja geometryczna liczb zespolonych

Podobnie jak liczby rzeczywiste można przedstawić za pomocą punktów na prostej liczbowej, tak liczby zespolone przedstawia się za pomocą punktów na płaszczyźnie zespolonej. Liczbę zespoloną $z = a + bi$ przedstawia punkt o odciętej (wartość rzeczywista) $a$ i rzędnej (wartość urojona) $b$. W ten sposób każdej liczbie zespolonej odpowiada jednoznacznie określony punkt na płaszczyźnie, zwanej płaszczyzną zespoloną.

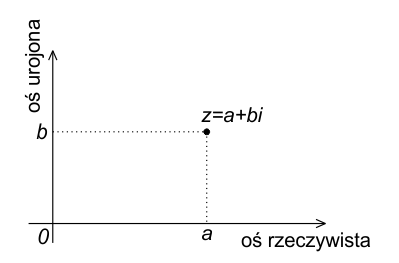
Oś rzeczywista i oś urojona

Na płaszczyźnie zespolonej liczby rzeczywiste są przedstawione za pomocą punktów na osi poziomej, zwanej osią rzeczywistą (oś odciętych). Liczby urojone, natomiast, są przedstawione za pomocą punktów na osi pionowej, zwanej osią urojoną (oś rzędnych). Każda liczba zespolona $z = a + bi$ może być więc traktowana jako punkt $(a, b)$ na tej płaszczyźnie, gdzie $a$ to część rzeczywista, a $b$ to część urojona liczby zespolonej.

Reprezentacja liczby zespolonej jako wektora

Ponieważ każdy punkt na płaszczyźnie może być wyznaczony przez wektor wodzący, łączący początek układu współrzędnych (zwany biegunem) z tym punktem, każdej liczbie zespolonej odpowiada określony wektor na płaszczyźnie. Wektor ten prowadzi od początku układu współrzędnych do punktu odpowiadającego danej liczbie zespolonej $z = a + bi$. Dzięki temu liczby zespolone mogą być przedstawiane nie tylko jako punkty, ale również jako wektory na płaszczyźnie zespolonej.

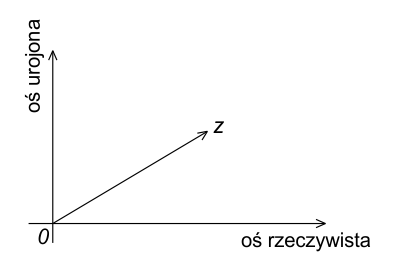
Znaczenie interpretacji geometrycznej

Interpretacja geometryczna liczb zespolonych jako punktów lub wektorów na płaszczyźnie ma wiele praktycznych zastosowań w matematyce i fizyce. Pozwala na wizualizację działań na liczbach zespolonych, takich jak dodawanie, odejmowanie, mnożenie czy dzielenie. Na przykład, dodawanie liczb zespolonych można zobrazować jako sumowanie odpowiednich wektorów, co ułatwia zrozumienie zjawisk związanych z rotacjami i przekształceniami geometrycznymi.

Liczby zespolone są również kluczowe w analizie matematycznej, gdzie umożliwiają badanie funkcji zespolonych i całkowania wzdłuż krzywych na płaszczyźnie zespolonej. W elektrotechnice, liczby zespolone są używane do analizy obwodów prądu zmiennego, gdzie jednostka urojona $i$ reprezentuje przesunięcie fazowe między napięciem a prądem.

Podsumowanie

Interpretacja geometryczna liczb zespolonych jako punktów i wektorów na płaszczyźnie zespolonej jest fundamentalnym pojęciem w matematyce. Umożliwia intuicyjne zrozumienie operacji na liczbach zespolonych i ma szerokie zastosowanie w wielu dziedzinach nauki i techniki.