Liczby zespolone sprzężone
Liczby zespolone sprzężone to pary liczb zespolonych, które mają równe części rzeczywiste i urojone o przeciwnych znakach. Liczbę zespoloną $z = a + bi$ oraz jej sprzężenie $\overline{z} = a - bi$ nazywamy liczbami sprzężonymi. Symbol $\overline{z}$ oznacza sprzężenie liczby zespolonej $z$. Sprzężenie liczby zespolonej jest operacją ważną w wielu zastosowaniach matematycznych, takich jak algebra liczb zespolonych, analiza matematyczna i elektrotechnika.
Definicja i notacja liczb zespolonych sprzężonych
Dwie liczby zespolone $z = a + bi$ oraz $\overline{z} = a - bi$ są sprzężone, jeśli ich części rzeczywiste są identyczne ($a = a$), a części urojone różnią się tylko znakiem ($b = -b$). Sprzężenie liczby zespolonej $z = a + bi$ jest oznaczane symbolem $\overline{z}$ i definiowane wzorem:
$$ \overline{z} = a - bi $$
Przykład: Jeśli $z = 3 + 4i$, to sprzężenie tej liczby jest $\overline{z} = 3 - 4i$. Część rzeczywista pozostaje taka sama (3), podczas gdy część urojona zmienia znak (z 4 na -4).
Interpretacja geometryczna liczb zespolonych sprzężonych
W interpretacji geometrycznej na płaszczyźnie zespolonej liczby zespolone sprzężone są symetryczne względem osi rzeczywistej (osi odciętych). Oznacza to, że punkty reprezentujące liczbę zespoloną $z = a + bi$ oraz jej sprzężenie $\overline{z} = a - bi$ leżą na linii poziomej, będącej odbiciem przez oś rzeczywistą.
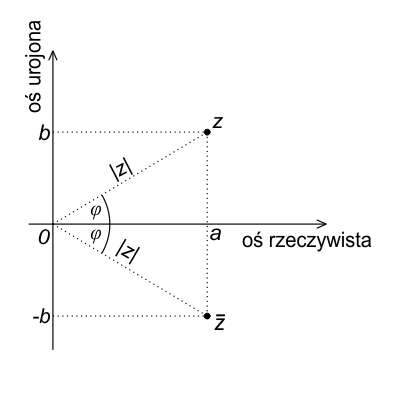
Jak widać na powyższym obrazku, liczba zespolona $z = a + bi$ i jej sprzężenie $\overline{z} = a - bi$ mają tę samą odciętą $a$, ale różnią się rzędną (jedna ma wartość $b$, a druga $-b$).
Właściwości liczb zespolonych sprzężonych
- Równość modułów: Moduł liczby zespolonej $z = a + bi$, oznaczany jako $|z|$, jest równy modułowi jej sprzężenia $\overline{z} = a - bi$. Oznacza to, że: $$ |z| = |\overline{z}| $$ Moduł liczby zespolonej to odległość punktu reprezentującego tę liczbę od początku układu współrzędnych.
- Suma i iloczyn liczb sprzężonych: Suma liczby zespolonej i jej sprzężenia jest liczbą rzeczywistą, natomiast iloczyn liczby zespolonej i jej sprzężenia jest kwadratem modułu tej liczby, a więc także liczbą rzeczywistą: $$ z + \overline{z} = (a + bi) + (a - bi) = 2a $$ $$ z \cdot \overline{z} = (a + bi)(a - bi) = a^2 - (bi)^2 = a^2 + b^2 = |z|^2 $$
- Sprzężenie sumy i iloczynu: Sprzężenie sumy dwóch liczb zespolonych jest równe sumie ich sprzężeń, a sprzężenie iloczynu jest równe iloczynowi ich sprzężeń: $$ \overline{z_1 + z_2} = \overline{z_1} + \overline{z_2} $$ $$ \overline{z_1 \cdot z_2} = \overline{z_1} \cdot \overline{z_2} $$
- Sprzężenie dzielenia: Sprzężenie ilorazu dwóch liczb zespolonych jest równe ilorazowi ich sprzężeń: $$ \overline{\left(\frac{z_1}{z_2}\right)} = \frac{\overline{z_1}}{\overline{z_2}} \quad \text{dla} \; z_2 \neq 0 $$
Znaczenie liczb zespolonych sprzężonych
Liczby zespolone sprzężone są niezwykle ważne w wielu dziedzinach matematyki i fizyki. W algebrze są wykorzystywane do rozkładania wielomianów na czynniki, w analizie zespolonej do badania funkcji zespolonych, a w elektrotechnice do analizy obwodów prądu zmiennego. W mechanice kwantowej liczby zespolone sprzężone są używane w opisach stanów kwantowych i operatorów hermitowskich.
Liczby sprzężone mają również zastosowanie w obliczeniach numerycznych, gdzie są używane do stabilizowania algorytmów i rozwiązywania równań różniczkowych oraz algebraicznych. Ich właściwości algebraiczne i geometryczne sprawiają, że są narzędziem niezwykle uniwersalnym i potężnym w matematyce.
Podsumowanie
Liczby zespolone sprzężone są parą liczb zespolonych, które mają równe części rzeczywiste i przeciwnie równe części urojone. Ich reprezentacja geometryczna na płaszczyźnie zespolonej pokazuje ich symetrię względem osi rzeczywistej. Właściwości i zastosowania liczb zespolonych sprzężonych są kluczowe w wielu obszarach matematyki i nauk stosowanych.