Trapez
Trapez to czworokąt, w którym przynajmniej dwa boki są do siebie równoległe. Te równoległe boki nazywamy podstawami trapezu. Trapez jest ważną figurą geometryczną, łączącą w sobie cechy równoległoboku i ogólnych czworokątów.
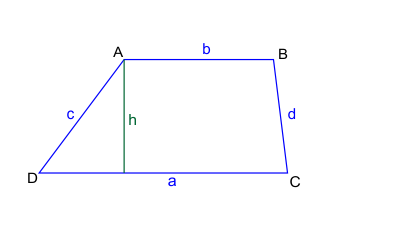
Elementy trapezu
Oznaczenia na rysunku:
- $a$ i $b$ - podstawy trapezu (boki równoległe)
- $c$ i $d$ - ramiona trapezu (boki nierównoległe)
- $h$ - wysokość trapezu
Wysokość $h$ jest opuszczona prostopadle do obu podstaw $a$ i $b$, tworząc kąt 90° z nimi.
Właściwości trapezu
- Posiada co najmniej jedną parę boków równoległych
- Suma kątów wewnętrznych wynosi 360°
- Przekątne dzielą się wzajemnie w stosunku zależnym od długości podstaw
Obliczenia związane z trapezem
Obwód trapezu
Obwód trapezu to suma długości wszystkich jego boków:
$$Obw=a+b+c+d$$
Pole powierzchni trapezu
Pole trapezu obliczamy korzystając ze wzoru:
$$P=\frac{1}{2}(a+b)h$$
Rodzaje trapezów
Trapez równoramienny
Trapez równoramienny to trapez mający ramiona równej długości.
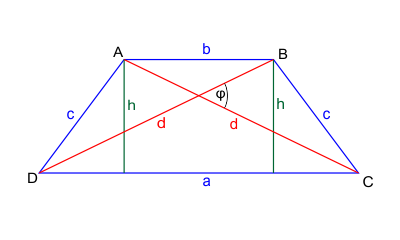
Dodatkowe właściwości trapezu równoramiennego:
- Kąty przy każdej podstawie są równe
- Przekątne są równej długości
- Można go wpisać w okrąg
Pole trapezu równoramiennego (niebędącego równoległobokiem) możemy obliczyć ze wzoru:
$$P=\frac{1}{2} d^2 \sin\varphi$$
gdzie:
$d$ - długość przekątnej trapezu (obie są jednakowej długości),
$\varphi$ - miara kąta pomiędzy przekątnymi trapezu.
Trapez prostokątny
Trapez prostokątny to trapez, w którym jedno z ramion tworzy z podstawą kąt prosty (90°).
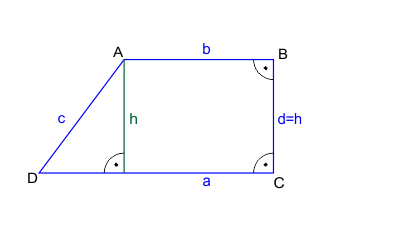
Szczególnym przypadkiem trapezu prostokątnego jest prostokąt, w którym oba ramiona tworzą z podstawami kąty proste.
Związek trapezu z innymi figurami geometrycznymi
Wiele innych czworokątów można uznać za szczególne przypadki trapezu:
Wszystkie te figury mają dwie pary równoległych boków, co czyni je szczególnymi przypadkami trapezów.
Zastosowania trapezu
Trapez znajduje zastosowanie w wielu dziedzinach:
- Architektura: w projektowaniu dachów i elementów konstrukcyjnych
- Inżynieria: w konstrukcjach mostów i innych struktur
- Optyka: w projektowaniu niektórych elementów optycznych
- Sztuka i design: jako element kompozycji wizualnych