Trójkąt prostokątny
Trójkąt prostokątny to taki trójkąt, który posiada jeden z kątów o mierze $90^\circ$ - czyli kąt prosty. Dwa boki przy kącie prostym tego trójkąta nazywane są przyprostokątnymi, natomiast bok leżący naprzeciw kąta prostego przeciwprostokątnym. Suma pozostałych kątów trójkąta wynosi $\alpha+\beta=90^\circ$.
Ilustracja
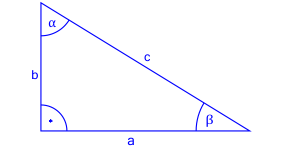
Elementy trójkąta prostokątnego
$a$ i $b$ - przyprostokątne - boki leżące przy kącie prostym,
$c$ - przeciwprostokątna - bok leżący naprzeciw kąta prostego,
$\alpha$ i $\beta$ - pozostałe dwa kąty trójkąta.
Kluczowe właściwości
- Suma miar kątów ostrych w trójkącie prostokątnym wynosi 90°.
- Przeciwprostokątna jest zawsze najdłuższym bokiem trójkąta prostokątnego.
- Wysokość opuszczona na przeciwprostokątną dzieli trójkąt prostokątny na dwa trójkąty podobne do trójkąta wyjściowego.
- W trójkącie prostokątnym środek okręgu opisanego znajduje się w połowie przeciwprostokątnej.
Twierdzenie Pitagorasa
Z trójkątem prostokątnym nierozerwalnie związane jest Twierdzenie Pitagorasa, które stwierdza, że suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej:
$$a^2 + b^2 = c^2$$
Funkcje trygonometryczne
Trójkąt prostokątny jest podstawą definicji funkcji trygonometrycznych dla kątów ostrych:
- $\sin \alpha = \frac{\text{przeciwprostokątna}}{\text{przeciwległa}} = \frac{a}{c}$
- $\cos \alpha = \frac{\text{przyległa}}{\text{przeciwprostokątna}} = \frac{b}{c}$
- $\tan \alpha = \frac{\text{przeciwległa}}{\text{przyległa}} = \frac{a}{b}$
Zastosowania
Trójkąty prostokątne mają szerokie zastosowanie w matematyce, fizyce, inżynierii i architekturze. Są używane do obliczania odległości, wysokości, kątów nachylenia oraz w projektowaniu konstrukcji.
Podsumowanie
Trójkąt prostokątny, mimo swojej prostoty, jest fundamentalną figurą w geometrii. Jego właściwości są kluczowe dla zrozumienia wielu koncepcji matematycznych i fizycznych. Umiejętność rozpoznawania i analizy trójkątów prostokątnych jest niezbędna w rozwiązywaniu problemów geometrycznych i trygonometrycznych.