Prostopadłościan

Prostopadłościan to graniastosłup foremny, w którym każda ze ścian jest prostokątem, a dwie dowolne ściany są prostopadłe lub równoległe do siebie. W związku z tym prostopadłościan charakteryzuje się prostymi kątami pomiędzy sąsiadującymi ścianami oraz równoległymi krawędziami w przeciwnych ścianach.

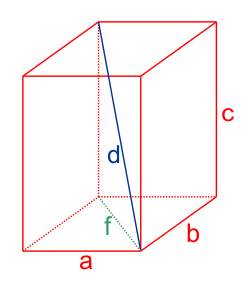
W prostopadłościanie oznaczamy:

• $a$, $b$ – krawędzie podstawy prostopadłościanu,
• $c$ – wysokość prostopadłościanu,
• $d$ – przekątną prostopadłościanu,
• $f$ – przekątną podstawy prostopadłościanu.

Pole powierzchni prostopadłościanu

Wzór na pole powierzchni prostopadłościanu to suma pól wszystkich jego ścian. Ponieważ każda ściana prostopadłościanu jest prostokątem, pole powierzchni można obliczyć, sumując pola par ścian:

$$ P = 2ab + 2ac + 2bc = 2(ab + ac + bc) $$

Objętość prostopadłościanu

Wszystkie ściany boczne prostopadłościanu są nachylone do podstawy pod kątem prostym. Dlatego objętość prostopadłościanu można obliczyć jako iloczyn długości trzech krawędzi wychodzących z jednego wierzchołka:

$$ V = abc $$

Długość przekątnej prostopadłościanu

Długość przekątnej prostopadłościanu można obliczyć, korzystając z Twierdzenia Pitagorasa. Najpierw obliczamy długość przekątnej podstawy, a następnie używamy tej wartości do obliczenia przekątnej całego prostopadłościanu:

$$ f = \sqrt{a^2 + b^2} $$

Ostatecznie wzór na długość przekątnej prostopadłościanu jest następujący:

$$ d = \sqrt{a^2 + b^2 + c^2} $$

Kula opisana na prostopadłościanie

Na prostopadłościanie można opisać kulę. Wzór na długość promienia kuli opisanej na prostopadłościanie jest następujący:

$$ R = \frac{1}{2}d = \frac{1}{2}\sqrt{a^2 + b^2 + c^2} $$

Ten wzór pokazuje, że promień kuli opisanej na prostopadłościanie zależy bezpośrednio od długości jego przekątnej, co jest logicznym następstwem faktu, że kula musi obejmować całą bryłę.