Wielościany

Wielościan to bryła geometryczna, której każda ze ścian jest wielokątem. Wielościany są podstawowym pojęciem w geometrii przestrzennej i znajdują zastosowanie w wielu dziedzinach, od architektury po informatykę.

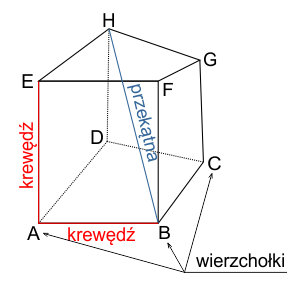
Elementy wielościanu

W każdym wielościanie można wyróżnić następujące elementy:

• Krawędzie – są to odcinki, które stanowią wspólne boki sąsiadujących ścian wielościanu.
• Wierzchołki – punkty, w których spotykają się krawędzie wielościanu.
• Przekątne – są to odcinki łączące dwa dowolne wierzchołki wielościanu, które nie należą do tej samej ściany.

Pole powierzchni wielościanu

Pole powierzchni wielościanu to suma pól wszystkich jego ścian. Dla każdego wielościanu foremnego istnieją wzory pozwalające obliczyć pole powierzchni na podstawie długości krawędzi. Przykład: Pole powierzchni sześcianu o krawędzi długości $a$ można obliczyć ze wzoru:

$$P=6a^2$$

Więcej informacji na temat obliczania pól powierzchni znajdziesz w artykule o wielościanach foremnych.

Objętość wielościanu

Objętość wielościanu to miara przestrzeni zajmowanej przez bryłę. W przypadku wielościanów foremnych, takich jak sześcian czy czworościan foremny, można skorzystać z gotowych wzorów. Przykładowo, objętość sześcianu o krawędzi długości $a$ obliczamy ze wzoru:

$$V=a^3$$

Dla wielościanów nieforemnych, objętość można obliczyć, dzieląc bryłę na mniejsze, znane wielościany foremne, których objętość da się obliczyć, a następnie sumując te objętości.

Więcej o obliczaniu objętości sześcianu oraz innych brył przeczytasz w sekcji poświęconej sześcianowi.

Przykład

Jeśli mamy bryłę, którą możemy podzielić na dwie piramidy o podstawach trójkątnych, możemy obliczyć objętość każdej z piramid i zsumować je, aby uzyskać objętość całego wielościanu.

Dodatkowo, możesz zapoznać się z różnymi metodami obliczania objętości brył, w tym ostrosłupów, które również są rodzajem wielościanów.

Praktyczne zastosowania wielościanów

Wielościany są nie tylko teoretycznym pojęciem w matematyce. Znajdują one zastosowanie w wielu dziedzinach, takich jak:

• Architektura – konstrukcja budynków i mostów często opiera się na strukturach wielościennych.
• Grafika komputerowa – modelowanie trójwymiarowe w programach komputerowych często bazuje na wielościanach.
• Inżynieria – w projektowaniu i analizie wytrzymałości konstrukcji.

Podsumowanie

Wielościany to fundamentalne bryły geometryczne, które charakteryzują się ścianami w postaci wielokątów. Umiejętność obliczania pola powierzchni i objętości wielościanów ma kluczowe znaczenie w wielu dziedzinach nauki i techniki. Warto poznać metody analizy tych brył zarówno dla ich praktycznych zastosowań, jak i dla rozwijania umiejętności geometrycznych.