Ekstremum i monotoniczność funkcji kwadratowej

Funkcja kwadratowa posiada dokładnie jedno ekstremum, które występuje w punkcie będącym wierzchołkiem wykresu funkcji kwadratowej, czyli paraboli. Współrzędne wierzchołka paraboli można obliczyć za pomocą wzorów:

$$W\left(\frac{-b}{2a}, \frac{-\Delta}{4a}\right)$$

gdzie $\Delta = b^2 - 4ac$. Zatem ekstremum funkcji kwadratowej ma wartość $ \frac{-\Delta}{4a} $ dla argumentu $ \frac{-b}{2a} $.

To, czy funkcja kwadratowa w wierzchołku paraboli przyjmuje wartość maksimum, czy minimum, zależy od wartości współczynnika $a$.

Maksimum i Minimum Funkcji Kwadratowej

Wartość współczynnika $a$ decyduje o kierunku ramion paraboli oraz o tym, czy ekstremum jest wartością maksymalną czy minimalną:

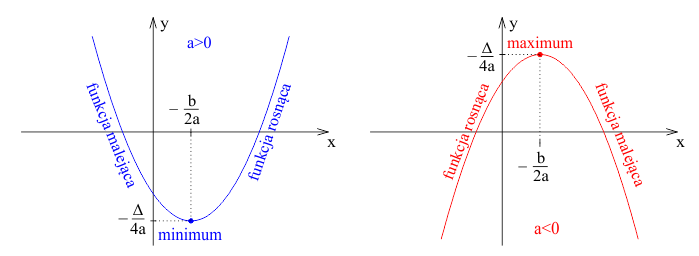
• Jeśli $a > 0$, ramiona paraboli skierowane są w górę, a funkcja kwadratowa w wierzchołku paraboli przyjmuje najmniejszą wartość, czyli minimum.
• Jeśli $a < 0$, ramiona paraboli skierowane są w dół, a funkcja kwadratowa w wierzchołku paraboli przyjmuje najwyższą wartość, czyli maksimum.

Monotoniczność Funkcji Kwadratowej

Monotoniczność funkcji kwadratowej również zależy od współczynnika $a$:

• Jeśli $a > 0$, ramiona paraboli skierowane są w górę. Wtedy funkcja kwadratowa jest malejąca w przedziale $x \in (-\infty, \frac{-b}{2a})$, osiąga minimum w punkcie $x = \frac{-b}{2a}$, a następnie jest rosnąca w przedziale $x \in (\frac{-b}{2a}, +\infty)$.
• Jeśli $a < 0$, ramiona paraboli skierowane są w dół. Wtedy funkcja kwadratowa jest rosnąca w przedziale $x \in (-\infty, \frac{-b}{2a})$, osiąga maksimum w punkcie $x = \frac{-b}{2a}$, a następnie jest malejąca w przedziale $x \in (\frac{-b}{2a}, +\infty)$.

Podsumowanie

Ekstremum i monotoniczność funkcji kwadratowej są ściśle związane z wartością współczynnika $a$. Zrozumienie tych właściwości jest kluczowe dla analizy funkcji kwadratowej i jej zastosowań w różnych dziedzinach matematyki oraz nauk technicznych.