Deltoid

Deltoid to czworokąt, który charakteryzuje się osią symetrii przechodzącą przez dwa przeciwległe wierzchołki. W deltoidzie jedna z przekątnych zawiera się w osi symetrii i jest jednocześnie symetralną drugiej przekątnej. Przekątne deltoidu przecinają się pod kątem prostym, czyli pod kątem $90^\circ$. Warto również zauważyć, że romb jest szczególnym przypadkiem deltoidu, w którym wszystkie boki są równej długości.

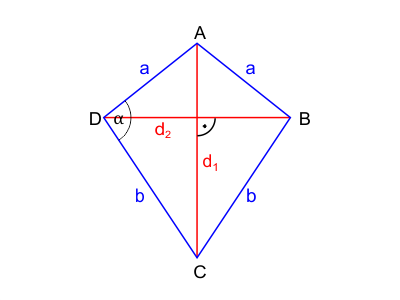
Oznaczenia i definicje

W deltoidzie używamy następujących oznaczeń:

• $a$ i $b$ – długości boków deltoidu,
• $d_1$ i $d_2$ – długości przekątnych deltoidu,
• $\alpha$ – miara kąta zawartego pomiędzy dwoma bokami o różnej długości.

Obwód deltoidu – wzór

Obwód deltoidu możemy obliczyć za pomocą prostego wzoru, sumując długości wszystkich jego boków:

$$Obw = 2a + 2b$$

Wzór ten wynika z faktu, że w deltoidzie dwa przeciwległe boki mają taką samą długość.

Pole powierzchni deltoidu – wzory

Pole powierzchni deltoidu można wyznaczyć na dwa różne sposoby:

• Za pomocą przekątnych: Pole deltoidu to połowa iloczynu długości przekątnych. Wzór ten jest szczególnie użyteczny, gdy znamy długości przekątnych deltoidu.
• Za pomocą boków i kąta: Pole deltoidu można również obliczyć jako iloczyn długości dwóch sąsiednich boków o różnej długości oraz sinusa kąta zawartego między nimi.

Oto wzory na pole deltoidu:

$$P = \frac{1}{2} d_1 \cdot d_2$$

$$P = a \cdot b \cdot \sin\alpha$$

Oba wzory są równoważne i można je stosować w zależności od dostępnych danych.

Zastosowanie deltoidu

Deltoid jest często spotykany w geometrii oraz w praktycznych zastosowaniach, takich jak projektowanie struktur architektonicznych, analiza sił w mechanice oraz w sztuce. Dzięki swojej osi symetrii i unikalnym właściwościom, deltoid stanowi interesujący obiekt badań matematycznych.

Podsumowując, deltoid to nie tylko ciekawy czworokąt o specyficznych właściwościach, ale także figura, której zrozumienie i znajomość wzorów umożliwia efektywne rozwiązywanie problemów geometrycznych.