Sześcian

Sześcian to szczególny przypadek prostopadłościanu, który jest jednocześnie graniastosłupem foremnym. Wszystkie ściany sześcianu są identycznymi kwadratami, co sprawia, że sześcian ma bardzo regularną strukturę i symetrię.

Pole powierzchni sześcianu

Wszystkie ściany sześcianu są identycznymi kwadratami, dlatego pole powierzchni sześcianu można obliczyć, mnożąc pole jednej ściany przez sześć:

$$ P = 6a^2 $$

Objętość sześcianu

Objętość sześcianu jest równa sześcianowi długości jednej krawędzi, ponieważ wszystkie krawędzie sześcianu są równej długości:

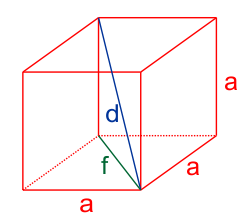
$$ V = a^3 $$

Długość przekątnej sześcianu

Długość przekątnej sześcianu można obliczyć przy użyciu Twierdzenia Pitagorasa. Najpierw obliczamy długość przekątnej dowolnej ściany, a następnie wykorzystujemy ją do obliczenia przekątnej całego sześcianu:

$$ f = \sqrt{a^2 + a^2} = \sqrt{2a^2} = a\sqrt{2} $$

Ostatecznie wzór na długość przekątnej sześcianu wygląda następująco:

$$ d = \sqrt{f^2 + a^2} = \sqrt{2a^2 + a^2} = \sqrt{3a^2} = a\sqrt{3} $$

Kula opisana na sześcianie i kula wpisana w sześcian

Sześcian jest bryłą, na której można opisać kulę, a także można w sześcian wpisać kulę. W przypadku kuli wpisanej, promień jest równy połowie długości krawędzi sześcianu:

$$ \text{Promień kuli wpisanej} = \frac{1}{2}a $$

Jeśli chodzi o kulę opisaną na sześcianie, promień tej kuli jest równy połowie długości przekątnej sześcianu:

$$ \text{Promień kuli opisanej} = \frac{1}{2}d = \frac{1}{2}a\sqrt{3} $$