Prostokąt
Prostokąt jest to czworokąt o czterech kątach wewnętrznych prostych oraz przeciwległych bokach równej długości. Jest to jedna z podstawowych figur geometrycznych, często spotykana w codziennym życiu i mająca szerokie zastosowanie w matematyce, architekturze i inżynierii.
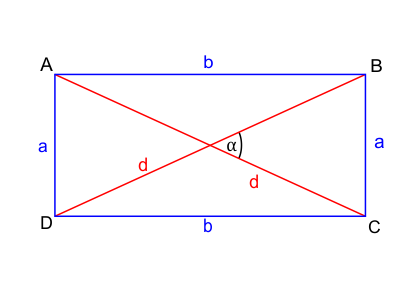
Elementy prostokąta
Objaśnienie oznaczeń na rysunku:
- $A$, $B$, $C$, $D$ - wierzchołki prostokąta
- $a$, $b$ - długości boków prostokąta
- $d$ - długość przekątnych prostokąta
- $\alpha$ - miara kąta zawartego pomiędzy przekątnymi
Własności prostokąta
- Wszystkie kąty wewnętrzne są proste (90°)
- Przeciwległe boki są równoległe i równej długości
- Przekątne są równej długości i przecinają się w połowie
- Prostokąt jest osiowo symetryczny względem prostych przechodzących przez środki przeciwległych boków
- Prostokąt jest środkowo symetryczny względem punktu przecięcia przekątnych
Obliczenia związane z prostokątem
Obwód prostokąta
Obwód prostokąta liczymy sumując długości wszystkich boków:
$$Obw=2a+2b$$
Pole powierzchni prostokąta
Pole prostokąta można obliczyć na dwa sposoby:
- Korzystając z długości boków:
$$P=ab$$
- Korzystając z długości przekątnej i kąta między przekątnymi:
$$P=\frac{1}{2}d^2\sin\alpha$$
Długość przekątnej
Długość przekątnej można wyliczyć korzystając z Twierdzenia Pitagorasa:
$$d=\sqrt{a^2+b^2}$$
Zastosowania prostokąta
Prostokąt znajduje szerokie zastosowanie w różnych dziedzinach:
- Architektura: projektowanie budynków, okien, drzwi
- Inżynieria: konstruowanie maszyn i urządzeń
- Sztuka: kompozycja obrazów, projektowanie graficzne
- Codzienne życie: kształt książek, ekranów, stołów
Powiązane zagadnienia
Aby lepiej zrozumieć właściwości prostokąta, warto zapoznać się z następującymi tematami:
- Czworokąt
- Kwadrat (szczególny przypadek prostokąta)
- Okrąg opisany na prostokącie
Zrozumienie właściwości prostokąta jest kluczowe dla dalszego studiowania geometrii i jej praktycznych zastosowań.