Pole trójkąta

Pole trójkąta można obliczyć na kilka sposobów. Wybór odpowiedniego wzoru zależy od tego, jakimi danymi dysponujemy. Poniżej przedstawiamy różne metody obliczania pola trójkąta w zależności od dostępnych informacji.

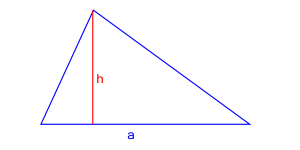
1. Znamy długość boku i długość wysokości opuszczonej na ten bok

Jeśli znamy długość boku trójkąta $a$ oraz długość wysokości $h$ opuszczonej na ten bok, pole trójkąta można obliczyć za pomocą wzoru:

$$P = \frac{1}{2}ah$$

gdzie:

$a$ - długość dowolnego boku trójkąta
$h$ - długość wysokości opuszczonej na bok $a$

pole trójkąta podstawa wysokość

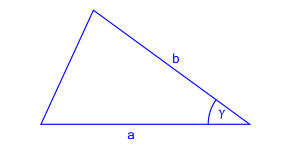
2. Znamy długości dwóch boków i miarę kąta zawartego między nimi

Jeśli znamy długości dwóch boków $a$ i $b$ oraz miarę kąta $\gamma$ zawartego między nimi, pole trójkąta można obliczyć za pomocą wzoru:

$$P = \frac{1}{2}ab\sin\gamma$$

gdzie:

$a$ i $b$ - długości dwóch sąsiednich boków
$\gamma$ - miara kąta wewnętrznego pomiędzy bokami $a$ i $b$

pole trójkąta dwa boki i sinus kąta między nimi

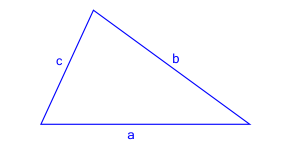
3. Znamy długości trzech boków trójkąta

Jeśli znamy długości trzech boków $a$, $b$ i $c$, pole trójkąta można obliczyć za pomocą wzoru Herona:

$$P = \sqrt{p(p-a)(p-b)(p-c)}$$

gdzie:

$a$, $b$, $c$ - długości boków trójkąta
$p$ - połowa obwodu trójkąta: $$p = \frac{a+b+c}{2}$$

pole trójkąta trzy boki i obwód

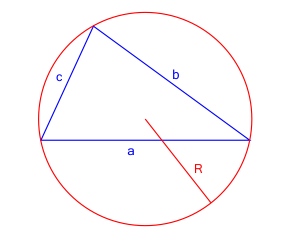
4. Znamy długość promienia okręgu opisanego na trójkącie i długości boków trójkąta

Jeśli znamy długości boków $a$, $b$ i $c$ oraz długość promienia $R$ okręgu opisanego na trójkącie, pole trójkąta można obliczyć za pomocą wzoru:

$$P = \frac{abc}{4R}$$

gdzie:

$a$, $b$, $c$ - długości boków trójkąta
$R$ - długość promienia okręgu opisanego na trójkącie

pole trójkąta trzy boki i promień okręgu opisanego

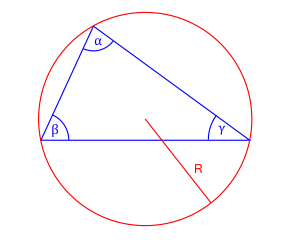
5. Znamy miary kątów wewnętrznych trójkąta i długość promienia okręgu opisanego

Jeśli znamy miary kątów wewnętrznych $\alpha$, $\beta$, $\gamma$ oraz długość promienia $R$ okręgu opisanego na trójkącie, pole trójkąta można obliczyć za pomocą wzoru:

$$P = 2R^2\sin\alpha\sin\beta\sin\gamma$$

gdzie:

$\alpha$, $\beta$, $\gamma$ - miary kątów wewnętrznych trójkąta
$R$ - długość promienia okręgu opisanego na trójkącie

pole trójkąta trzy kąty i promień okręgu opisanego

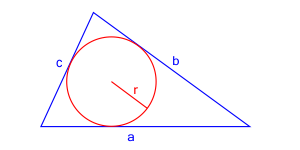
6. Znamy długość promienia okręgu wpisanego w trójkąt i długości boków trójkąta

Jeśli znamy długości boków $a$, $b$ i $c$ oraz długość promienia $r$ okręgu wpisanego w trójkąt, pole trójkąta można obliczyć za pomocą wzoru:

$$P = \frac{1}{2}r(a+b+c)$$

gdzie:

$a$, $b$, $c$ - długości boków trójkąta
$r$ - długość promienia okręgu wpisanego w trójkąt

pole trójkąta trzy boki i promień okręgu wpisanego

Podsumowanie

Różnorodność metod obliczania pola trójkąta pokazuje elastyczność i bogactwo geometrii. Wybór odpowiedniej metody zależy od dostępnych danych i konkretnej sytuacji. Znajomość tych wzorów jest niezbędna w wielu dziedzinach, od podstawowej geometrii po zaawansowane zastosowania w fizyce i inżynierii.