Monotoniczność funkcji liniowej

Monotoniczność funkcji liniowej zależna jest od wartości współczynnika kierunkowego $a$ w równaniu $f(x)=ax+b$. Funkcja liniowa może być rosnąca, malejąca lub stała w całej swojej dziedzinie.

Rodzaje monotoniczności

1. Jeżeli współczynnik kierunkowy $a>0$ - funkcja w całej swojej dziedzinie jest rosnąca.
2. Jeżeli współczynnik kierunkowy $a<0$ - funkcja w całej swojej dziedzinie jest malejąca.
3. Jeżeli współczynnik kierunkowy $a=0$ - funkcja w całej swojej dziedzinie jest stała.

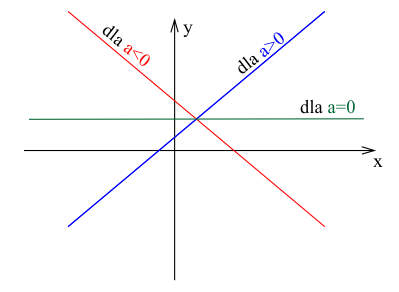
Interpretacja geometryczna

• Dla $a>0$: wykres funkcji "wznosi się" w prawo
• Dla $a<0$: wykres funkcji "opada" w prawo
• Dla $a=0$: wykres funkcji jest linią poziomą, równoległą do osi OX

Własności monotoniczności

• Funkcja liniowa jest monotoniczna w całej swojej dziedzinie (cały zbiór liczb rzeczywistych $\mathbb{R}$).
• Monotoniczność jest ścisła dla $a\ne 0$ (funkcja ściśle rosnąca lub ściśle malejąca).
• Funkcja liniowa nie posiada ekstremów lokalnych ani globalnych (z wyjątkiem funkcji stałej, gdzie każdy punkt jest ekstremum).

Przykłady

Przykład 1: $f(x)=2x+3$

$a=2>0$, więc funkcja jest rosnąca.

Przykład 2: $f(x)=-0.5x+1$

$a=-0.5<0$, więc funkcja jest malejąca.

Przykład 3: $f(x)=4$

$a=0$, więc funkcja jest stała.

Znaczenie monotoniczności

Monotoniczność funkcji liniowej ma istotne znaczenie w wielu dziedzinach:

• Matematyka: Pomaga w analizie zachowania funkcji i rozwiązywaniu nierówności.
• Fizyka: Opisuje zależności liniowe, np. ruch jednostajny.
• Ekonomia: Modeluje trendy w cenach, kosztach, czy popycie.
• Statystyka: Jest kluczowa w analizie regresji liniowej.

Powiązane koncepcje

• Wartość bezwzględna współczynnika $a$ określa "stromość" funkcji.
• Kąt nachylenia prostej do osi OX jest związany z wartością współczynnika $a$ (tangens tego kąta).
• Monotoniczność funkcji liniowej jest podstawą do zrozumienia monotoniczności bardziej złożonych funkcji.

Podsumowanie

Monotoniczność funkcji liniowej jest jedną z jej kluczowych cech, bezpośrednio związaną ze współczynnikiem kierunkowym $a$. Zrozumienie monotoniczności jest fundamentalne dla analizy zachowania funkcji, interpretacji wykresów i rozwiązywania problemów w różnych dziedzinach nauki. Prostota funkcji liniowej sprawia, że jest ona idealnym wprowadzeniem do koncepcji monotoniczności, która staje się bardziej złożona dla funkcji nieliniowych.