Odejmowanie liczb zespolonych

Odejmowanie dwóch liczb zespolonych jest operacją arytmetyczną, w której od jednej liczby zespolonej odejmujemy drugą, traktując osobno ich części rzeczywiste i urojone. Jeśli mamy dwie liczby zespolone $z_1 = a_1 + b_1i$ oraz $z_2 = a_2 + b_2i$, to różnica tych liczb, $z = z_1 - z_2$, jest określona wzorem:

$$ z_1 - z_2 = (a_1 + b_1i) - (a_2 + b_2i) = (a_1 - a_2) + (b_1 - b_2)i $$

W tym wzorze:

• $a_1$ i $a_2$ – części rzeczywiste liczb zespolonych $z_1$ i $z_2$
• $b_1$ i $b_2$ – części urojone liczb zespolonych $z_1$ i $z_2$

Aby odjąć dwie liczby zespolone, należy odjąć ich części rzeczywiste oraz części urojone:

$$ (a_1 - a_2) \quad \text{i} \quad (b_1 - b_2)i $$

Interpretacja geometryczna odejmowania liczb zespolonych

Odejmowanie liczb zespolonych ma intuicyjne wyjaśnienie geometryczne na płaszczyźnie zespolonej. Każdą liczbę zespoloną $z = a + bi$ można przedstawić jako punkt lub wektor na płaszczyźnie zespolonej, gdzie $a$ jest współrzędną rzeczywistą (oś x), a $b$ współrzędną urojoną (oś y).

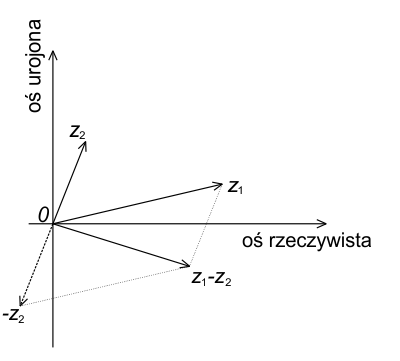
Odejmowanie liczby zespolonej $z_2$ od liczby zespolonej $z_1$ można interpretować jako dodanie do wektora reprezentującego $z_1$ wektora przeciwnego do $z_2$. W praktyce oznacza to przesunięcie punktu końcowego wektora $z_1$ w kierunku przeciwnym do wektora $z_2$. Wektor różnicy $z = z_1 - z_2$ jest zatem wektorem łączącym końce wektorów $z_2$ i $z_1$.

Przykład odejmowania liczb zespolonych

Rozważmy kilka przykładów odejmowania liczb zespolonych:

• Przykład 1: Odejmijmy liczby zespolone $z_1 = 5 + 3i$ oraz $z_2 = 2 + 4i$. Różnica tych liczb to: $$ z_1 - z_2 = (5 + 3i) - (2 + 4i) = (5 - 2) + (3 - 4)i = 3 - i $$
• Przykład 2: Odejmijmy liczby zespolone $z_1 = -1 + 2i$ oraz $z_2 = 3 - 6i$. Różnica tych liczb to: $$ z_1 - z_2 = (-1 + 2i) - (3 - 6i) = (-1 - 3) + (2 + 6)i = -4 + 8i $$

Właściwości odejmowania liczb zespolonych

Odejmowanie liczb zespolonych ma kilka ważnych właściwości, podobnych do właściwości odejmowania liczb rzeczywistych:

• Przeciwdodawanie: Odejmowanie można interpretować jako dodanie liczby przeciwnej. Dla dowolnych liczb zespolonych $z_1$ i $z_2$: $$ z_1 - z_2 = z_1 + (-z_2) $$ gdzie $-z_2$ jest liczbą przeciwną do $z_2$.
• Rozdzielność względem dodawania: Odejmowanie liczb zespolonych jest rozdzielne względem dodawania. Dla dowolnych liczb zespolonych $z_1$, $z_2$ i $z_3$: $$ (z_1 - z_2) - z_3 = z_1 - (z_2 + z_3) $$
• Istnienie elementu neutralnego: Liczba zespolona $0 + 0i$ jest elementem neutralnym odejmowania, co oznacza, że: $$ z - 0 = z $$ dla dowolnej liczby zespolonej $z$.

Podsumowanie

Odejmowanie liczb zespolonych polega na odjęciu odpowiednich części rzeczywistych i urojonych. Operacja ta jest analogiczna do odejmowania liczb rzeczywistych i jest użyteczna w analizie zespolonej oraz wielu zastosowaniach praktycznych. Znajomość tej operacji jest niezbędna do pracy z liczbami zespolonymi w matematyce, fizyce i inżynierii.