Wykres funkcji logarytmicznej
Wykresem funkcji logarytmicznej jest krzywa logarytmiczna. Jest ona zwierciadlanym odbiciem krzywej wykładniczej względem prostej $y=x$. Ta symetria wynika z faktu, że funkcja logarytmiczna jest funkcją odwrotną do funkcji wykładniczej.
Kluczowe cechy wykresu funkcji logarytmicznej:
- Dziedzina: Funkcja logarytmiczna istnieje tylko dla $x > 0$. Wynika to z definicji logarytmu, który jest określony tylko dla liczb dodatnich.
- Punkt przecięcia z osią OX: Wykres zawsze przechodzi przez punkt (1, 0), niezależnie od podstawy logarytmu.
- Asymptota pionowa: Oś OY ($x = 0$) jest asymptotą pionową wykresu. Krzywa zbliża się do niej tym szybciej, im większa jest wartość $|\ln a|$, gdzie $a$ jest podstawą logarytmu.
- Ciągłość: Funkcja logarytmiczna jest ciągła w całej swojej dziedzinie.
- Różnowartościowość: Każda wartość $y$ odpowiada dokładnie jednej wartości $x$, co czyni funkcję logarytmiczną funkcją różnowartościową.
Wykres funkcji logarytmicznej dla $a > 1$
Gdy podstawa logarytmu $a$ jest większa od 1, funkcja logarytmiczna jest rosnąca. Jej wykres ma następujące cechy:
- Funkcja jest ściśle rosnąca
- Wartości funkcji rosną od $-\infty$ (gdy $x$ zbliża się do 0 od prawej strony) do $+\infty$ (gdy $x$ rośnie nieograniczenie)
- Wykres jest wypukły, co oznacza, że tempo wzrostu maleje wraz ze wzrostem $x$
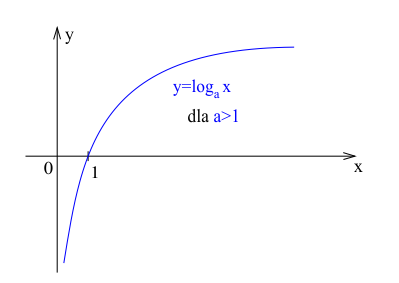
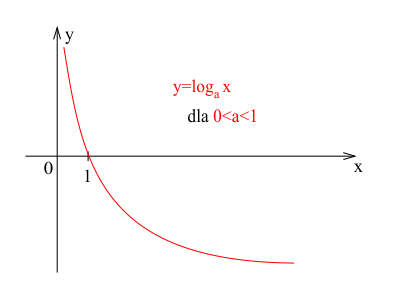
Wykres funkcji logarytmicznej dla $0 < a < 1$
Gdy podstawa logarytmu $a$ znajduje się między 0 a 1, funkcja logarytmiczna jest malejąca. Jej wykres charakteryzuje się następującymi cechami:
- Funkcja jest ściśle malejąca
- Wartości funkcji maleją od $+\infty$ (gdy $x$ zbliża się do 0 od prawej strony) do $-\infty$ (gdy $x$ rośnie nieograniczenie)
- Wykres jest wklęsły, co oznacza, że tempo spadku maleje wraz ze wzrostem $x$
Szczególne przypadki
- Logarytm naturalny Wykres funkcji $f(x) = \ln x$ (logarytm o podstawie $e \approx 2.71828$) jest często używany jako reprezentatywny przykład funkcji logarytmicznej.
- Logarytm dziesiętny: Wykres funkcji $f(x) = \log_{10} x$ jest powszechnie stosowany w naukach przyrodniczych i inżynierii ze względu na wygodę w obliczeniach.
Wykres funkcji logarytmicznej, ze swoją charakterystyczną formą, pozwala na wizualizację i analizę wielu zjawisk naturalnych i procesów, szczególnie tych, które wykazują szybki wzrost lub spadek w początkowej fazie, a następnie stabilizują się lub zwalniają.