Wykres funkcji liniowej
Wykresem funkcji liniowej jest prosta. Kształt i położenie tej prostej na płaszczyźnie kartezjańskiej zależą od wartości współczynników $a$ i $b$ w równaniu $y = ax + b$.
Wpływ współczynników na wykres
Współczynnik kierunkowy $a$
Od współczynnika kierunkowego $a$ zależy kierunek prostej oraz jej nachylenie do osi X:
- Gdy $a > 0$, funkcja jest rosnąca, a prosta nachylona jest w prawo (w górę).
- Gdy $a < 0$, funkcja jest malejąca, a prosta nachylona jest w lewo (w dół).
- Gdy $a = 0$, funkcja jest stała, a prosta jest równoległa do osi X.
Im większa wartość bezwzględna $|a|$, tym bardziej stroma jest prosta.
Wyraz wolny $b$
Wyraz wolny $b$ określa punkt przecięcia prostej z osią Y:
- Gdy $b > 0$, prosta przecina oś Y powyżej początku układu współrzędnych.
- Gdy $b < 0$, prosta przecina oś Y poniżej początku układu współrzędnych.
- Gdy $b = 0$, prosta przechodzi przez początek układu współrzędnych (0,0).
Graficzna interpretacja
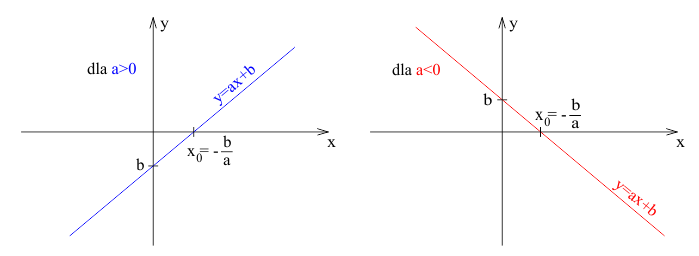
Na powyższym rysunku widoczne są dwa przykłady wykresów funkcji liniowej:
- Po lewej stronie: funkcja rosnąca (dla $a > 0$)
- Po prawej stronie: funkcja malejąca (dla $a < 0$)
Kluczowe punkty na wykresie
Miejsce zerowe
Miejsce zerowe funkcji liniowej to punkt przecięcia wykresu z osią X. Jego współrzędna x wynosi:
$$x_0 = -\frac{b}{a}$$
To miejsce jest zaznaczone na obu wykresach jako $x_0$.
Punkt przecięcia z osią Y
Punkt przecięcia z osią Y ma zawsze współrzędne $(0, b)$, gdzie $b$ to wyraz wolny funkcji.
Interpretacja geometryczna współczynników
- $a$ - tangens kąta nachylenia prostej do osi OX
- $b$ - rzędna punktu przecięcia prostej z osią OY
Przykłady
Przykład 1: $y = 2x + 3$
- Funkcja rosnąca ($a > 0$)
- Przecina oś Y w punkcie (0, 3)
- Miejsce zerowe: $x_0 = -\frac{3}{2} = -1.5$
Przykład 2: $y = -x - 1$
- Funkcja malejąca ($a < 0$)
- Przecina oś Y w punkcie (0, -1)
- Miejsce zerowe: $x_0 = -\frac{-1}{-1} = -1$
Podsumowanie
Wykres funkcji liniowej, mimo swojej prostoty, niesie ze sobą wiele informacji o samej funkcji. Umiejętność interpretacji tego wykresu i rozumienie wpływu współczynników $a$ i $b$ na jego kształt i położenie są kluczowe w analizie matematycznej, fizyce, ekonomii i wielu innych dziedzinach nauki. Wykres funkcji liniowej stanowi również podstawę do zrozumienia bardziej złożonych funkcji i ich wykresów.