Ostrosłup prawidłowy trójkątny

Ostrosłup prawidłowy trójkątny to taki ostrosłup, którego podstawą jest trójkąt foremny, czyli trójkąt równoboczny. W takim ostrosłupie wysokość poprowadzona jest ze środka podstawy, czyli punktu przecięcia się dwusiecznych trójkąta, które pełnią również funkcję wysokości i środkowych. Ściany boczne tego ostrosłupa są identycznymi trójkątami równoramiennymi, co nadaje ostrosłupowi symetrię i regularność.

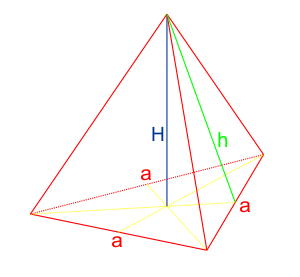
Pole powierzchni ostrosłupa prawidłowego trójkątnego

Pole powierzchni ostrosłupa to suma pól ścian bocznych oraz pola podstawy. Dla ostrosłupa prawidłowego trójkątnego pole powierzchni obliczamy według wzoru:

$$ P = P_b + P_p = 3 \times \frac{1}{2}ah + \frac{a^2\sqrt{3}}{4} = \frac{3ah}{2} + \frac{a^2\sqrt{3}}{4} $$

gdzie:

• $P_b$ – suma wszystkich pól ścian bocznych ostrosłupa,
• $P_p$ – pole podstawy ostrosłupa,
• $a$ – długość boku podstawy (trójkąta równobocznego),
• $h$ – wysokość ściany bocznej ostrosłupa.

Objętość ostrosłupa prawidłowego trójkątnego

Objętość ostrosłupa wyrażona jest jako iloczyn jednej trzeciej pola podstawy i wysokości ostrosłupa. Dla ostrosłupa prawidłowego trójkątnego wzór na objętość wygląda następująco:

$$ V = \frac{1}{3}P_p \cdot H = \frac{1}{3} \times \frac{a^2\sqrt{3}}{4} \times H = \frac{a^2H\sqrt{3}}{12} $$

gdzie:

• $P_p$ – pole podstawy ostrosłupa (trójkąta równobocznego),
• $H$ – wysokość ostrosłupa, czyli odległość od wierzchołka do płaszczyzny podstawy.

Ostrosłupy prawidłowe trójkątne, dzięki swojej symetrii i regularności, znajdują zastosowanie w wielu dziedzinach, od architektury po sztukę, a ich właściwości geometryczne są szeroko analizowane w matematyce.