Zadanie 14
Tangens kąta $\alpha$ zaznaczonego na rysunku jest równy:
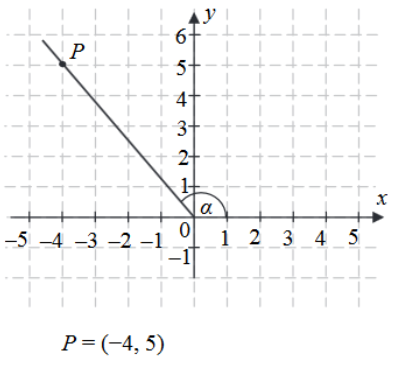
B. $-\frac{4}{5}$
C. $-1$
D. $-\frac{5}{4}$
Aby rozwiązać to zadanie, musimy skorzystać z właściwości funkcji liniowej oraz definicji tangensa kąta. Współczynnik kierunkowy funkcji liniowej jest równy tangensowi kąta, jaki tworzy ta prosta z osią $ x $. Tangens kąta $ \alpha $ można zdefiniować jako stosunek przyrostu wartości $ y $ do przyrostu wartości $ x $ między dwoma punktami na prostej.
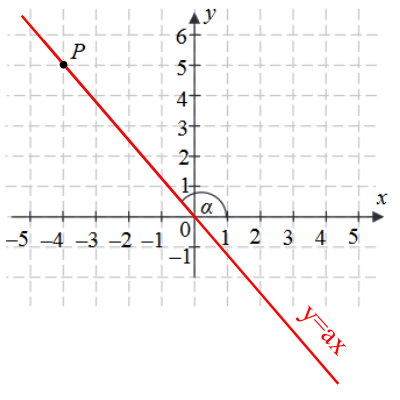
Znając dwa punkty, przez które przechodzi prosta: punkt $ (0, 0) $ oraz punkt $ P = (-4, 5) $, możemy obliczyć współczynnik kierunkowy $ a $ tej prostej, który jest równy tangensowi kąta $ \alpha $.
1. Obliczenie współczynnika kierunkowego.
Współczynnik kierunkowy $ a $ obliczamy ze wzoru:
$$a = \frac{y_2 - y_1}{x_2 - x_1}.$$
Podstawiając wartości punktów $ (x_1, y_1) = (0, 0) $ oraz $ (x_2, y_2) = (-4, 5) $, otrzymujemy:
$$a = \frac{5 - 0}{-4 - 0} = \frac{5}{-4} = -\frac{5}{4}.$$
2. Określenie wartości tangensa kąta $ \alpha $.
Z powyższych obliczeń wynika, że współczynnik kierunkowy $ a $ jest równy $ -\frac{5}{4} $. Oznacza to, że tangens kąta $ \alpha $ między prostą a osią $ x $ wynosi:
$$\tan \alpha = -\frac{5}{4}.$$
Wniosek:
Odpowiedź, która odpowiada obliczonemu współczynnikowi kierunkowemu i wartości tangensa, to D.