Zadanie 22

Aby rozwiązać to zadanie, musimy skorzystać z wzoru na objętość stożka oraz zastosować Twierdzenie Pitagorasa do wyznaczenia wysokości stożka.

Rozwiązanie:

1. Wzór na objętość stożka.

Objętość stożka możemy obliczyć za pomocą wzoru:

$$V = \frac{1}{3} \pi r^2 h,$$

gdzie $ r $ to promień podstawy stożka, a $ h $ to wysokość stożka.

2. Analiza przekroju osiowego stożka.

Przekrojem osiowym stożka jest trójkąt równoboczny o boku długości $ 6 $. W trójkącie równobocznym wszystkie boki są równej długości, więc tworząca stożka $ l $ wynosi $ 6 $. Promień podstawy stożka $ r $ to połowa długości boku trójkąta równobocznego, więc:

$$r = \frac{1}{2} \cdot l = \frac{1}{2} \cdot 6 = 3.$$

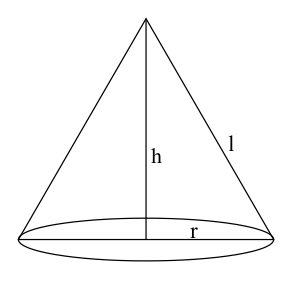
3. Obliczenie wysokości stożka za pomocą Twierdzenia Pitagorasa.

Wysokość stożka $ h $ możemy obliczyć, stosując Twierdzenie Pitagorasa w trójkącie prostokątnym utworzonym przez wysokość stożka, promień podstawy i tworzącą. Twierdzenie Pitagorasa mówi, że:

$$r^2 + h^2 = l^2.$$

Podstawiamy znane wartości $ r = 3 $ oraz $ l = 6 $:

$$h^2 = l^2 - r^2 = 6^2 - 3^2 = 36 - 9 = 27.$$

Obliczamy wysokość $ h $:

$$h = \sqrt{27} = \sqrt{9 \cdot 3} = 3\sqrt{3}.$$

4. Obliczenie objętości stożka.

Mając już wszystkie potrzebne dane, podstawiamy je do wzoru na objętość stożka:

$$V = \frac{1}{3} \pi \cdot r^2 \cdot h = \frac{1}{3} \pi \cdot 3^2 \cdot 3\sqrt{3}.$$

Obliczamy dalej:

$$V = \frac{1}{3} \pi \cdot 9 \cdot 3\sqrt{3} = 3 \cdot 3 \pi \sqrt{3} = 9\pi\sqrt{3}.$$

Wniosek:

Objętość stożka wynosi $ 9\pi\sqrt{3} $. Odpowiedzią do zadania jest B.