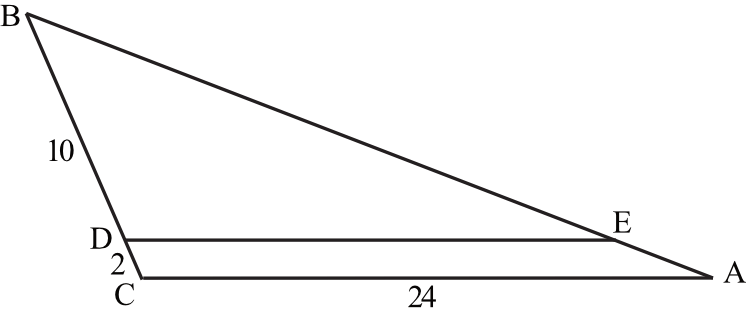
Skoro odcinek $DE$ jest równoległy do boku $AC$, to trójkąty $ABC$ oraz $EBD$ są trójkątami podobnymi (na mocy cechy kąt-kąt-kąt). Stosunek długości odpowiadających sobie boków tych trójkątów będzie taki sam.
Możemy zapisać równanie opisujące stosunek boków:
$$ \frac{|DE|}{|AC|} = \frac{|BD|}{|BC|} $$
Podstawiając dane z zadania:
$$ \frac{|DE|}{24} = \frac{10}{10 + 2} $$
Upraszczając wyrażenie, otrzymujemy:
$$ \frac{|DE|}{24} = \frac{10}{12} $$
Aby znaleźć $|DE|$, mnożymy obie strony równania przez 24:
$$ |DE| = \frac{10 \cdot 24}{12} $$
$$ |DE| = \frac{240}{12} $$
$$ |DE| = 20 $$
Zatem długość odcinka $DE$ jest równa $20$. Poprawna odpowiedź to B.