Zadanie 17
(1pkt)
Obwód trójkąta przedstawionego na rysunku jest równy: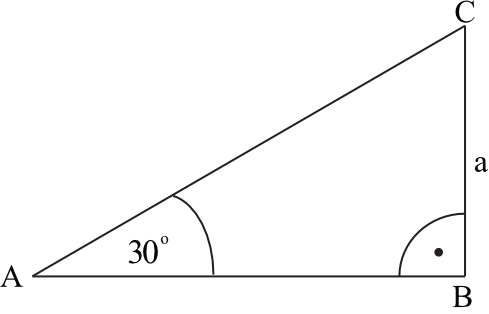
B. $\left(2+\frac{\sqrt{2}}{2}\right)a$
C. $(3+\sqrt{3})a$
D. $(2+\sqrt{2})a$
Rozwiązanie
(1pkt)
Obwód trójkąta przedstawionego na rysunku jest równy:
W tym zadaniu najprościej będzie wykorzystać własności trójkątów o kątach $30^\circ$, $60^\circ$, $90^\circ$. Z tych własności wynika wprost, że długość dłuższej przyprostokątnej jest równa $|AB| = a\sqrt{3}$, a długość przeciwprostokątnej wynosi $|AC| = 2a$.
Obwód trójkąta będzie więc równy:
$$ \text{Obw} = a + a\sqrt{3} + 2a $$
$$ \text{Obw} = 3a + a\sqrt{3} $$
$$ \text{Obw} = (3 + \sqrt{3})a $$
Zatem obwód trójkąta jest równy $(3 + \sqrt{3})a$. Poprawna odpowiedź to C.
Gdybyśmy nie pamiętali o tych własnościach, możemy zawsze posłużyć się funkcjami trygonometrycznymi, aby wyznaczyć długości boków:
Skorzystamy z funkcji tangens:
$$ \tan30^\circ = \frac{a}{|AB|} $$
$$ \frac{\sqrt{3}}{3} = \frac{a}{|AB|} \quad \bigg/ \cdot |AB| $$
$$ a = \frac{\sqrt{3}}{3}|AB| \quad \bigg/ \cdot \frac{3}{\sqrt{3}} $$
$$ |AB| = \frac{3}{\sqrt{3}}a $$
$$ |AB| = \frac{3\sqrt{3}}{3}a $$
$$ |AB| = a\sqrt{3} $$
Skorzystamy z funkcji sinus:
$$ \sin30^\circ = \frac{a}{|AC|} $$
$$ \frac{1}{2} = \frac{a}{|AC|} \quad \bigg/ \cdot |AC| $$
$$ a = \frac{1}{2}|AC| \quad \bigg/ \cdot 2 $$
$$ |AC| = 2a $$
Obliczenia te potwierdzają nasze wcześniejsze wnioski dotyczące długości boków trójkąta.
Aby zapewnić jak najlepsze wrażenia, korzystamy z technologii, takich jak pliki cookie, do przechowywania i/lub uzyskiwania dostępu do informacji o urządzeniu. Zgoda na te technologie pozwoli nam przetwarzać dane, takie jak zachowanie podczas przeglądania lub unikalne identyfikatory na tej stronie. Brak wyrażenia zgody lub wycofanie zgody może niekorzystnie wpłynąć na niektóre cechy i funkcje.