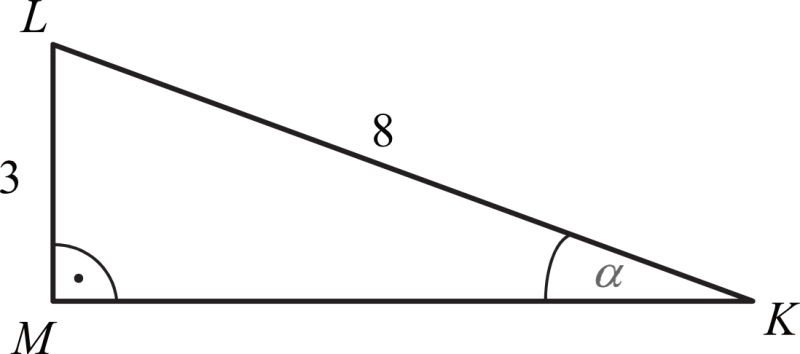
W tym zadaniu mamy trójkąt prostokątny i musimy znaleźć miarę kąta ostrego $α$, używając informacji o długościach jego boków.
Obliczenie wartości sinusa kąta $α$.
Znamy długość przyprostokątnej leżącej naprzeciw kąta $α$, oznaczonej jako $|LM|$, oraz długość przeciwprostokątnej, oznaczonej jako $|LK|$. W trójkącie prostokątnym wartość sinusa kąta $α$ możemy obliczyć, dzieląc długość przyprostokątnej przez długość przeciwprostokątnej:
$$
\sin α = \frac{|LM|}{|LK|}
$$
Podstawiając dane z treści zadania, gdzie $|LM| = 3$ i $|LK| = 8$, otrzymujemy:
$$
\sin α = \frac{3}{8}
$$
Odczytanie miary kąta z tablic matematycznych.
Aby znaleźć miarę kąta $α$, musimy poszukać w tablicach matematycznych, dla jakiego kąta ostrego wartość sinusa jest najbliższa lub równa $\frac{3}{8}$. Wartość $\frac{3}{8}$ to dokładnie $0.375$.
Sprawdzając tablice, widzimy, że dla kąta $22°$ wartość sinusa wynosi $0.3746$, co jest bardzo bliskie $0.375$. Na tej podstawie możemy przyjąć, że kąt $α$ leży w przedziale $21° < α \leq 24°$.
Zatem prawidłową odpowiedzią jest zakres kątów, w którym znajduje się $22°$, czyli $21° < α \leq 24°$.