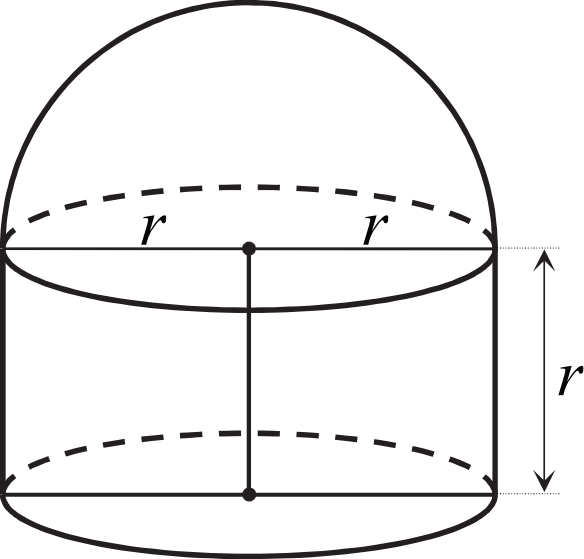
W tym zadaniu mamy do czynienia z bryłą złożoną z walca i półkuli, gdzie wysokość walca oraz promień półkuli są równe. Aby znaleźć objętość całej bryły, musimy najpierw obliczyć objętość każdej z części osobno.
Obliczenie objętości walca:
Wzór na objętość walca jest dany przez:
$$
V_w = P_p \cdot h
$$
gdzie $P_p$ to pole podstawy walca, a $h$ to jego wysokość. W naszym przypadku podstawa walca jest kołem o promieniu $r$, a wysokość walca jest równa $r$. Stąd:
$$
P_p = πr^2
$$
$$
V_w = πr^2 \cdot r = πr^3
$$
Objętość walca wynosi więc $πr^3$.
Obliczenie objętości półkuli:
Objętość pełnej kuli o promieniu $r$ wyraża się wzorem:
$$
V_k = \frac{4}{3}πr^3
$$
Ponieważ mamy do czynienia z półkulą, objętość półkuli $V_p$ jest połową objętości pełnej kuli:
$$
V_p = \frac{1}{2} \cdot \frac{4}{3}πr^3 = \frac{2}{3}πr^3
$$
Obliczenie objętości całej bryły:
Całkowita objętość bryły $V$ jest sumą objętości walca i półkuli:
$$
V = V_w + V_p
$$
Podstawiając wartości $V_w$ i $V_p$, otrzymujemy:
$$
V = πr^3 + \frac{2}{3}πr^3
$$
Aby uprościć to wyrażenie, zauważamy, że możemy dodać te dwie objętości, traktując $πr^3$ jako wspólny czynnik:
$$
V = \left(1 + \frac{2}{3}\right)πr^3 = \frac{5}{3}πr^3
$$
Zatem objętość całej bryły wynosi $\frac{5}{3}πr^3$. Wynik ten pokazuje, jak łącząc objętości walca i półkuli, możemy obliczyć całkowitą objętość bardziej złożonych brył.