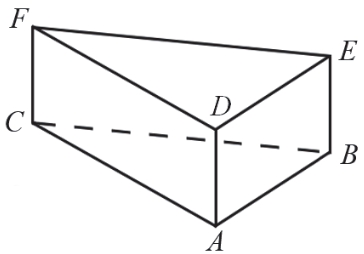
Dane:
- Graniastosłup prawidłowy trójkątny
- Pole powierzchni całkowitej: $45\sqrt{3}$
- Pole podstawy = pole ściany bocznej
Cel: Obliczyć objętość graniastosłupa.
Rozwiązanie:
1. Obliczenie pola podstawy
Oznaczmy pole podstawy jako $P_p$ i pole ściany bocznej jako $P_{śb}$. Wiemy, że $P_p = P_{śb}$.
Pole powierzchni całkowitej: $P_c = 2P_p + 3P_{śb} = 5P_p = 45\sqrt{3}$
Stąd: $P_p = \frac{45\sqrt{3}}{5} = 9\sqrt{3}$
2. Obliczenie długości krawędzi podstawy
Dla trójkąta równobocznego o boku $a$: $P_p = \frac{a^2\sqrt{3}}{4}$
$9\sqrt{3} = \frac{a^2\sqrt{3}}{4}$
$36 = a^2$
$a = 6$ (odrzucamy rozwiązanie ujemne)
3. Obliczenie wysokości graniastosłupa
Pole ściany bocznej: $P_{śb} = a \cdot H$, gdzie $H$ to wysokość graniastosłupa
$9\sqrt{3} = 6 \cdot H$
$H = \frac{3\sqrt{3}}{2}$
4. Obliczenie objętości graniastosłupa
$V = P_p \cdot H$
$V = 9\sqrt{3} \cdot \frac{3\sqrt{3}}{2}$
$V = \frac{27 \cdot 3}{2} = \frac{81}{2}$
Wniosek:
Objętość graniastosłupa wynosi $\frac{81}{2}$ jednostek sześciennych.
Weryfikacja:
Możemy sprawdzić nasze obliczenia, obliczając pole powierzchni całkowitej z otrzymanych wymiarów:
$P_c = 2P_p + 3P_{śb} = 2 \cdot 9\sqrt{3} + 3 \cdot 9\sqrt{3} = 45\sqrt{3}$
To zgadza się z danymi w zadaniu, co potwierdza poprawność naszych obliczeń.