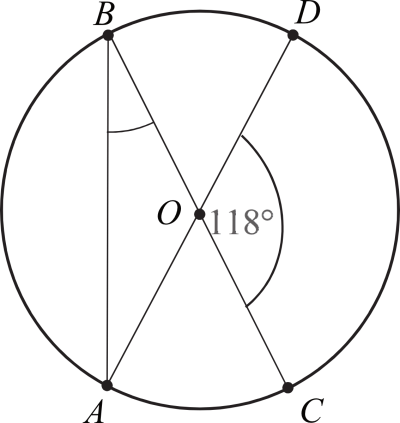
Aby obliczyć miarę kąta $ABC$, musimy najpierw znaleźć miarę kąta $BOA$ oraz skorzystać z własności trójkątów równoramiennych.
Rozwiązanie:
1. Obliczenie miary kąta $BOA$.
Kąt $BOA$ jest kątem wierzchołkowym względem kąta $DOC$. Kąty wierzchołkowe mają równe miary, zatem:
$$|\sphericalangle BOA| = 118°$$
2. Obliczenie miary kąta $ABC$.
Rozważmy trójkąt $ABO$, który jest trójkątem równoramiennym, ponieważ boki $BO$ i $AO$ są równe długości promienia okręgu. W trójkącie równoramiennym kąty przy podstawie są równe.
Skoro kąt $BOA$ ma miarę $118°$, to na dwa kąty przy podstawie pozostaje:
$$180° - 118° = 62°$$
Każdy z kątów przy podstawie ma więc miarę:
$$\frac{62°}{2} = 31°$$
To oznacza, że miara kąta $ABO$, a tym samym kąta $ABC$, wynosi $31°$.
Wniosek:
Miara kąta $ABC$ jest równa $31°$.