Zadanie 29
(2pkt)
Trójkąt $ABC$ jest równoboczny. Punkt $E$ leży na wysokości $CD$ tego trójkąta oraz $|CE|=\frac{3}{4}|CD|$. Punkt $F$ leży na boku $BC$ i odcinek $EF$ jest prostopadły do $BC$ (zobacz rysunek).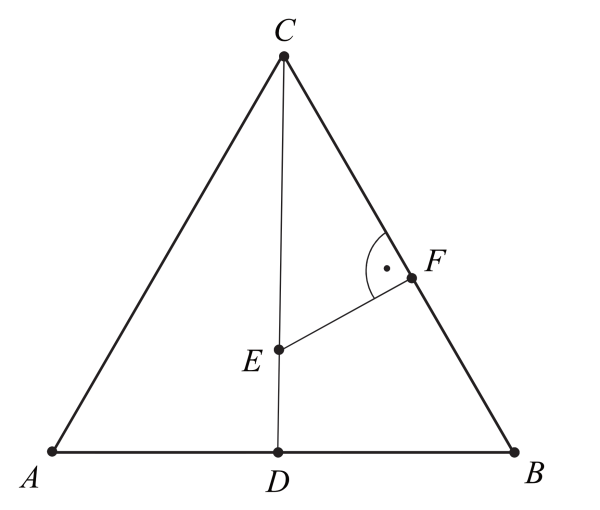
Wykaż, że $|CF|=\frac{9}{16}|CB|$.
Aby rozwiązać to zadanie, musimy przeanalizować długości odcinków oraz podobieństwo trójkątów w trójkącie równobocznym.
Rozwiązanie:
1. Obliczenie długości odcinka $CE$.
Z własności trójkąta równobocznego wiemy, że wysokość $h$ jest równa $\frac{a\sqrt{3}}{2}$. W związku z tym długość odcinka $CD$ wynosi $\frac{a\sqrt{3}}{2}$. Z treści zadania wynika, że odcinek $CE$ stanowi $\frac{3}{4}$ długości odcinka $CD$, więc możemy zapisać:
$$|CE| = \frac{3}{4} |CD|$$
$$|CE| = \frac{3}{4} \cdot \frac{a\sqrt{3}}{2}$$
$$|CE| = \frac{3\sqrt{3}a}{8}$$
2. Ustalanie podobieństwa trójkątów $CEF$ i $CDB$.
Spójrzmy na trójkąty $CEF$ oraz $CDB$. Oba trójkąty są prostokątne, co oznacza, że mają jeden kąt prosty. Mają również wspólny kąt $ECF$, co oznacza, że dwa kąty w obu trójkątach są równe. W związku z tym trzeci kąt w obu trójkątach musi być również równy. Z tego wynika, że zgodnie z zasadą kąt-kąt-kąt, trójkąty $CEF$ i $CDB$ są podobne.
3. Wyznaczenie długości odcinka $CF$ na podstawie podobieństwa trójkątów.
Skoro trójkąty $CEF$ oraz $CDB$ są podobne, możemy ułożyć proporcję:
$$\frac{|CF|}{|CD|} = \frac{|CE|}{|CB|}$$
Podstawiamy znane długości:
$$\frac{|CF|}{\frac{a\sqrt{3}}{2}} = \frac{\frac{3\sqrt{3}a}{8}}{a}$$
$$\frac{|CF|}{\frac{a\sqrt{3}}{2}} = \frac{3\sqrt{3}}{8}$$
Rozwiązując tę proporcję, otrzymujemy:
$$|CF| = \frac{3\sqrt{3}}{8} \cdot \frac{a\sqrt{3}}{2}$$
$$|CF| = \frac{3\sqrt{3} \cdot \sqrt{3} \cdot a}{8 \cdot 2}$$
$$|CF| = \frac{9a}{16} = \frac{9}{16}a$$
4. Zakończenie dowodzenia.
Długość $a$ jest długością każdego z boków trójkąta równobocznego, w tym boku $BC$. W naszych obliczeniach otrzymaliśmy, że $|CF| = \frac{9}{16} |BC|$, co jest zgodne z treścią zadania. Tym samym dowodzenie zostało zakończone.